Group Sequential Design (GSD)

Planning and design

Appropriateness

Whilst early stopping can offer several advantages (ethical, economic, and time-saving benefits), it is important to properly consider the impact of stopping part way through, and whether the data at this time point are sufficient to provide a good enough answer. The considerations will depend on the specific trial, but some key considerations, which also apply in other adaptive trials with early stopping options (e.g. of treatment options in MAMS trials) are: 

1) What are the costs of stopping early? 

By introducing interim analyses, GSDs require more management, timely data processing and statistical involvement. Are the costs of these worth it? Do the potential benefits exceed these costs, or are the expected benefits minimal? 

2) Interpreting studies which stop early 

Early stopping may raise questions in the interpretation especially when the effect of the intervention is known to be influenced by other factors. Examples of this vary, but include: 

  • seasonality: is the trial period done in a time frame which is favourable or unfavourable to the effect of the treatment? Would it work as well had it covered extended periods (e.g. both cold and warm seasons)? 
  • learning effect: did the trial end for futility before the trial team were fully versed in its delivery? 
  • follow-up duration: are the outcomes measured over a period long enough to convince readers of the value of the findings? 

3) Will the interim data be ready in time? 


This is probably the biggest single consideration: will the outcome data be collected in time to make a meaningful decision to stop? For instance, interim analyses may be rendered unnecessary if the recruitment rate is expected to be too fast with short treatment duration relative to the accrual of primary outcome data. It may also be impractical to implement the design in trials with prolonged treatment duration and long-term outcomes. 

4) Are interim data sufficient to inform early stopping? 

The availability of sufficient interim data to base early stopping decisions on is essential as it influences the interpretation of results. Furthermore, even though interim analyses are often based on the primary outcome data, the totality of interim data should be sufficient to address key research questions considered.

Design concepts

Traditionally, GSDs were developed focusing on comparing one new treatment to a comparator, although extensions have been made to accommodate multiple study treatments, for example in multi-arm multi-stage (MAMS) and adaptive population enrichment (APE) designs. The below focuses on introducing a GSD comparing one new treatment against a comparator and extensions are covered in their respective adaptive design sections. 

At the design stage, researchers decide on additional aspects that influence the GSD. These include: 

  • the criteria researchers wish to stop the trial early for (e.g., futility only, efficacy only, either futility or efficacy, non-inferiority, etc);
  • the appropriate stopping rules for making early trial stopping decisions;
  • measures of treatment effect (and when this is observed is important to inform early stopping); 
  • how many times interim data will be analysed (frequency of interim analyses);
  • when will interim data be analysed (timing of interim analyses).
The frequency and timing of interim analyses can be flexible when appropriate stopping rules are used, although pre-planning is essential for credibility to avoid looking like researchers are making things up as they go along (see general considerations) and to have control over the maximum sample size. The required maximum sample size (or the required maximum number of events for a time-to-event outcome) is the number needed if the study does not stop early. 

Once the time of the first interim analysis is reached, the interim primary outcome data are analysed and compared to the preset stopping rules. If the observed measure of treatment effect at this point crosses the threshold for stopping the trial (stopping boundary), then the trial is stopped based on having gathered sufficient evidence to make a conclusion. Otherwise, if the stopping boundaries have not been crossed (i.e., the treatment effect is within the continuation region), then researchers will continue to recruit more patients and proceed to the next planned analysis The same process is applied if second or subsequent interim analyses are undertaken, although the boundaries themselves may change. Each interim analysis uses all primary outcome data gathered until that point. 

Figure 1 is an example of a one-sided GSD planned with four interim analyses followed by a final analysis with options to stop the trial early for lack of benefit (futility) or benefit (efficacy). The vertical axis refers to the test statistic for the difference between treatment and control, and in this case a positive value favours the new treatment. The trial should be stopped early with sufficient evidence of treatment efficacy at the third interim analysis since this is when the observed interim treatment effect crossed the prespecified efficacy boundary (in this case the test statistic of 2.98 exceeds the threshold of 2.40).

Figure 1.

Figure 1. Example of a group sequential design with options to stop early for efficacy or futility. Note: cannot reject H0 and reject H0 could mean that no treatment difference has been established (or new treatment could be worse than the comparator) and researchers have concluded that the new treatment is better (more beneficial) than the comparator, respectively.

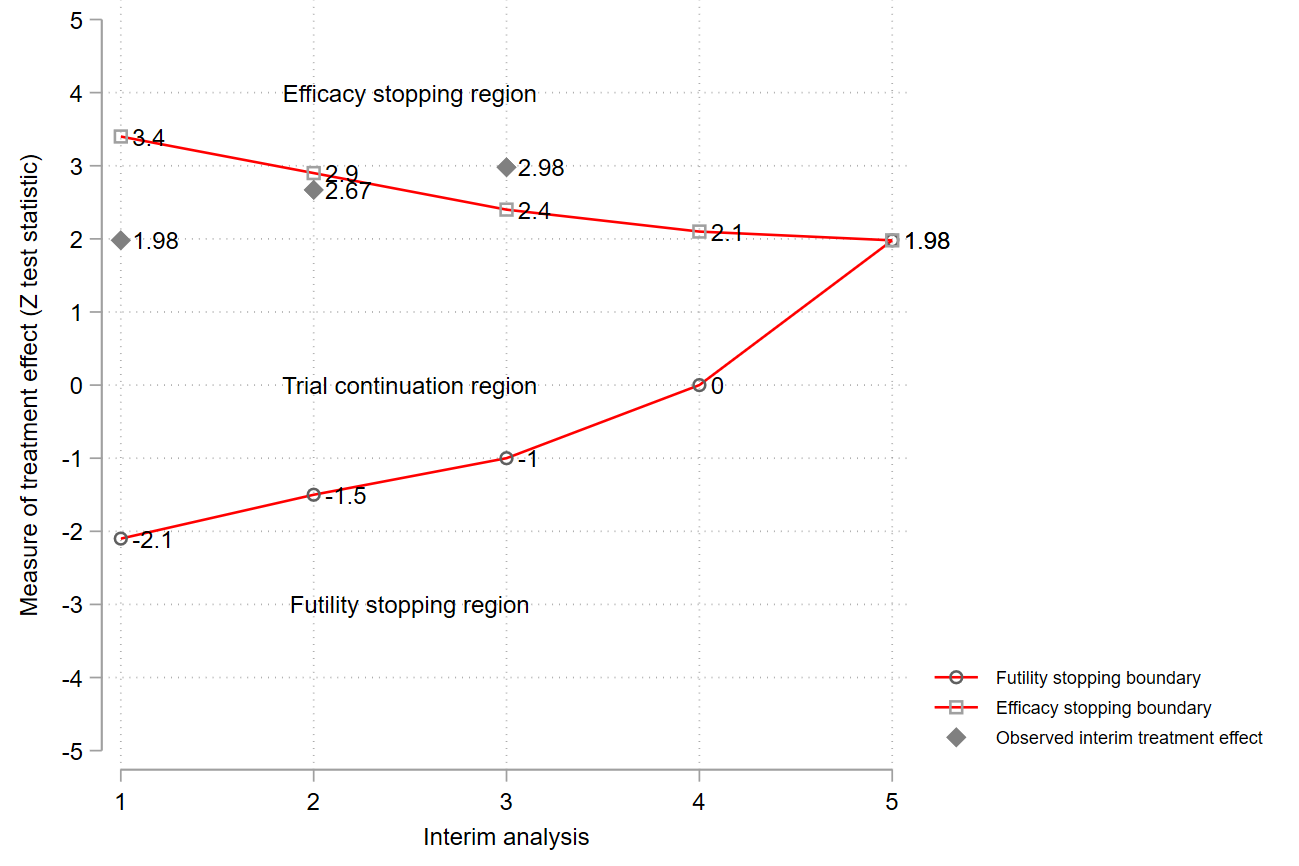
Example of a group sequential design with options to stop early for efficacy or futility. Note: cannot reject H0 and reject H0 could mean that no treatment difference has been established (or new treatment could be worse than the comparator) and researchers have concluded that the new treatment is better (more beneficial) than the comparator, respectively.

Note also that in addition to stopping early for efficacy, futility or non-inferiority, other adaptations can also be considered simultaneously. For example, the interim analysis may allow a sample size re-calculation, either on the basis of the interim treatment difference (an unblinded sample size recalculation) or other things such as withdrawal rate (a blinded recalculation). A trial may also stop on the basis of a safety concern, but typically this does not require formal stopping rules.

Prospective case studies

A GSD is the most common adaptive design and there are several examples of its use in randomised trials 1, 2, 3, 11 . Here, we provide a couple of examples.

1. MAPAC trial 4 

This study evaluated the effects of receiving an extract of Viscum album [L.] (VaL) or no antineoplastic therapy on overall survival of patients with locally advanced or metastatic cancer of the pancreas. Researchers designed this parallel-group, randomised trial as a GSD with an option to stop early for efficacy. Two interim analyses were planned after 220 (50%) and 320 (75%) patients followed by a final analysis at 428 (100%) patients. The primary outcome was overall survival at 12 months and researchers were targeting to prolong the median survival from 5 to 7 months, which is approximately equivalent to a hazard ratio of 0.714. They estimated the sample size assuming a power of 85% and type I error of 5% for a two-sided group sequential test, an accrual period of 53 months with an additional follow-up time of 12 months, a 1:1 allocation ratio, and a dropout rate of around 20%. A Lan-DeMets alpha spending function 5 that mimics the O’Brien and Fleming stopping rule 6 was used to define the stopping boundaries of the group sequential tests. The primary analysis of overall survival used the Cox proportional hazard model with treatment and prognosis groups as predictor variables to calculate the Z test statistic needed for making early stopping decisions. 

Researchers performed the first interim analysis after recruiting 220 patients (110 per arm). At this point, the median overall survival of patients was 4.8 and 2.7 months in the VaL and control groups, respectively. Although the researchers did not report the observed Z test statistic and the corresponding stopping boundary, they stated that an independent data monitoring committee (IDMC) recommended early stopping. They also recommended giving all study patients unrestricted access to VaL therapy because the interim results showed overwhelming effectiveness of VaL. Stagewise ordering statistical method 7 was used to compute the unbiased median estimate, the confidence interval for the prognosis-group adjusted hazard ratio, and corresponding p-value after early stopping. This produced a hazard ratio of 0.49 (95% confidence interval: 0.36 to 0.65, p-value < 0.0001) in favour of VaL. It should be noted that the interpretation of the results might be obscured because the distribution of how long patients were followed up for when the interim analysis was performed seems unclear. 

The benefits of using a GSD was that the trial was stopped early because there was sufficient evidence of the benefit of VaL and patients within and outside the trial received this effective treatment quicker. Furthermore, it also saved time and study resources since researchers stopped the trial halfway.  

Talking point: early stopping of survival trials is often challenging especially when median survival has not been reached at an interim analysis because early observed effects may not translate into late effects. 

2. REBOA trial 8,9

This trial investigated the effects of resuscitative endovascular balloon occlusion of the aorta (REBOA) treatment designed to reduce further blood loss and improve myocardial and cerebral perfusion (though at the cost of an ischemic debt) in trauma patients with confirmed or suspected life-threatening torso haemorrhage. This was a two-arm, parallel-group, individually randomised trial comparing standard of care plus REBOA and standard of care alone. The primary outcome, intended to capture potentially late harmful effects, is 90-day mortality defined as death within 90 days of injury, before or after discharge from hospital. 

The REBOA trial was designed as a Bayesian GSD 10 with options to stop early for futility at interim analyses. Researchers published details of its design and rationale with operating characteristics of the design 8. The GSD had three stages: two interim analyses after 40 and 80 randomised patients with outcome data (in total), and a final analysis after a maximum of 120 randomised patients were followed up. Researchers decided that the trial should be stopped early for harm (equivalent to futility in this case) of REBOA if there is a high posterior probability of at least 90% that the 90-day survival odds ratio falls below one at the first or second interim analysis. REBOA will be declared successful (effective and safe) if the probability of the 90-day survival odds ratio exceeds one at the final analysis by at least 95%. 

The planned statistical analysis (at interim and final) models 90-day survival on the log-odds scale using a logistic regression model with non-informative priors for the control and intervention survival proportions, and the treatment effect. Researchers assumed the treatment effect to be normally distributed on the log-odds scale with a known variance. As such, researchers will make decisions about stopping the trial early or declaring success based on probabilities derived from the normally distributed posterior distribution of the treatment effect on the log-odds scale. 

This trial is ongoing so what happened during the trial and decisions made by the researchers will be updated when it has been reported.

References

 1. Hatfield et al. Adaptive designs undertaken in clinical research: a review of registered clinical trials. Trials. 2016;17(1):150.
2. Sato et al. Practical characteristics of adaptive design in phase 2 and 3 clinical trials. J Clin Pharm Ther. 2017; 43(2) :1–11.
3. Todd et al. Interim analyses and sequential designs in phase III studies. Br J Clin Pharmacol. 2001;51(5):394–9.
4. Tröger et al. Viscum album [L.] extract therapy in patients with locally advanced or metastatic pancreatic cancer: a randomised clinical trial on overall survival. Eur J Cancer. 2013;49(18):3788–97.
5. Lan et al. Discrete sequential boundaries for clinical trials. Biometrika. 1983;70(3):659–63.
6. O’Brien et al. A multiple testing procedure for clinical trials. Biometrics. 1979;35(3):549–56.
7. Emerson et al. Parameter estimation following group sequential hypothesis testing. Biometrika. 1990;77(4):875–92.
8. Jansen et al. Bayesian clinical trial designs: Another option for trauma trials? Journal of Trauma and Acute Care Surgery. 2017;83(4): 736–41.
9. Jansen et al. UK-REBOA trial protocol. 2017.
10. Gerber et al. gsbDesign: An R package for evaluating the operating characteristics of a group sequential Bayesian design. J Stat Softw. 2016;69(11):1–23.
11. Judge et al. Trends in adaptive design methods in dialysis clinical trials: A systematic review. Kidney Med. 2021;3(6):925–41. 

Underpinning statistical methods

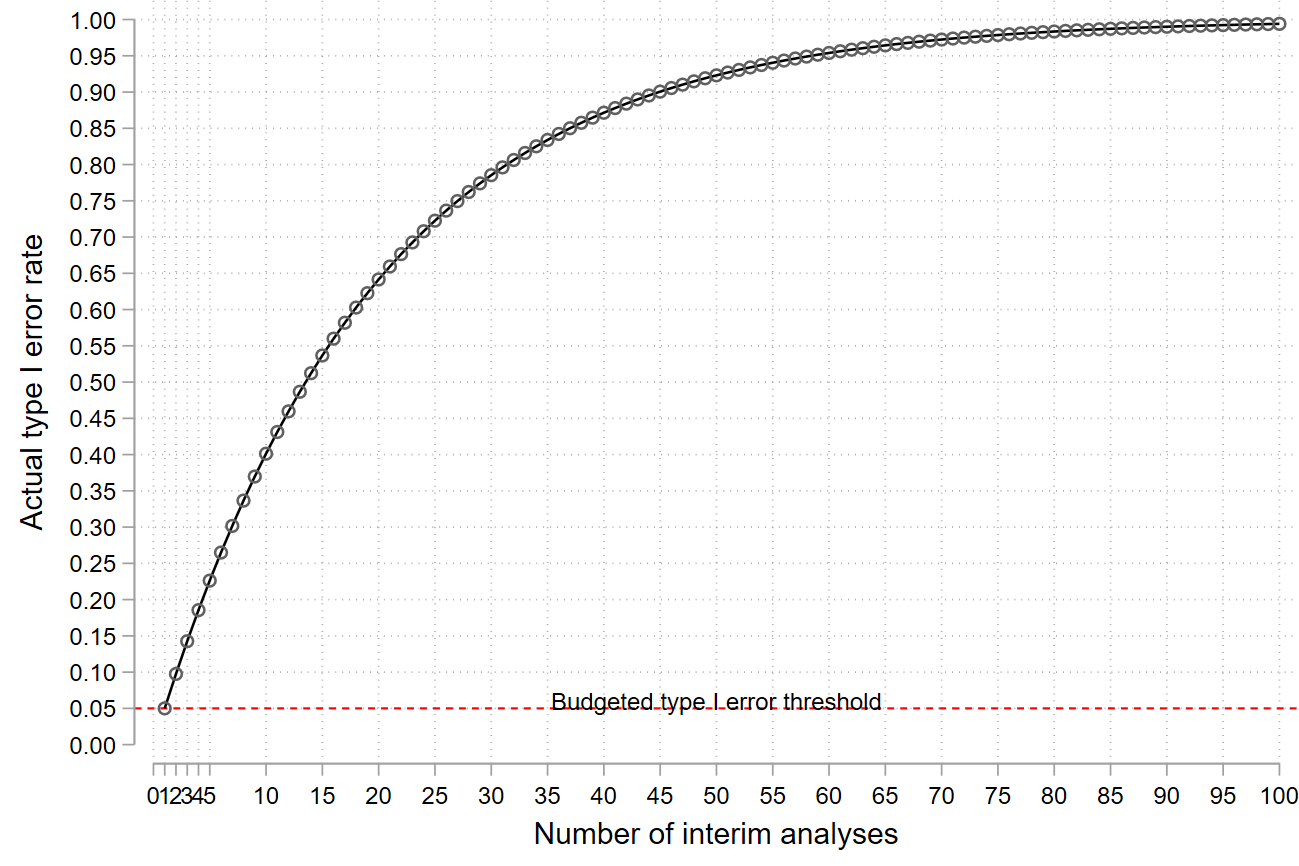
The main statistical issue arises from the fact that early stopping decisions are made based on analyses of outcome data at multiple timepoints. This increases the chances of making incorrect conclusions such as declaring the treatment to be beneficial when in fact it is not. This risk increases with an increasing number of interim analyses 1. Put another way, if researchers were to undertake two interim analyses (in addition to the final analysis) each at the 5% significance level, there is a greater than 5% chance of finding a significant difference for an ineffective treatment on at least one of them (in fact, it is 9.75%). Figure 2 illustrates the increase in the chances of finding a false-positive result as the number of data looks increases.

Figure 2.

Figure 2. Figure 2. Impact of repeated hypothesis testing on the type I error rate.

Impact of repeated hypothesis testing on the type I error rate.

GSD methods address this by raising the bar of the level of evidence researchers need to claim the evidence at interim and final analyses. The stopping rules are set in a way that does not compromise the type I error or false discovery rate. Typically, the type I error of a non-GSD trial is 5%: to match this, each analysis (interim or final) within a GSD needs a p-value lower than 5% in order to produce a 5% chance that an ineffective treatment will cross the stopping boundary at any point in the trial. Whilst GSDs therefore penalise a trial for performing multiple analyses and early trial stopping decisions, the gains can be substantial. 

GSDs are constructed to ensure that the desired operating characteristics (e.g., type I and type II errors or decision errors) are controlled at the desired levels. Researchers define the stopping rules or how they would want to spend the budgeted risks or errors for making wrong decisions at each interim and planned final analysis (during the entire trial). These stopping rules can be presented on different scales that can be easily understood by stakeholders (e.g., treatment effect, test statistic, p-value, error spend, posterior probabilities, conditional or predictive probabilities) 2, 3, 4, 5, 16, 17. Theoretically, the interim test statistics from accumulating outcome data for assessing interim treatment effects are correlated with a known joint distribution. Thus, we can work out the total sample size required given the number of interim analyses and their timing, the stopping rules, the joint distribution of the interim test statistics, and desired error rates to preserve. Several authors have developed many stopping boundaries from a statistical perspective 6. These boundaries differ concerning aspects such as the scope of early stopping they allow 7, their shape that relates to the level of evidence that is needed for early stopping, and ability to offer flexibility in the timing and frequency of interim analyses (which are not data-driven). Of note, some stopping boundaries are unified functions in the sense that they can mimic other rules when parameters that influence their shape are changed 6, 7, 8, 9. 

The stopping rules do not necessarily need to be formalised statistical functions but can be clinically defined by researchers to suit their research context. In other settings (e.g., restricted population), the stopping boundaries can be calculated for a given feasible maximum sample size and other operating characteristics that researchers would want to control for (e.g., overall type I error and statistical power). Bayesian GSDs are constructed using the same principles with a focus on posterior probabilities of the treatment effect being above a certain clinical effect of interest 10, 11, 12, 13. 

Group sequential methods have recently been extended to incorporate monitoring the primary outcome and a key secondary outcome simultaneously through the derivation of primary and secondary boundaries including a modified approach for interim decision-making 14. 

Key message

In some cases, stopping boundaries need to be reset (for current and future interim analyses) if the timing or the number of interim analysis fails to correspond to what was planned for some reason. For example, sometimes recruitment can be faster than anticipated thus more patients may contribute to the interim analysis than anticipated, rendering a planned interim analysis unnecessary, or an external data monitoring committee may rightly request a formal additional interim analysis after the accrual of a certain number of patients (e.g., see 15). In such cases, if a flexible stopping rule was used (e.g., error spending functions), the stopping boundaries can be reset to match interim data and account for additional analyses. 

References

1. Armitage et al. Repeated significance tests on accumulating data. J R Stat. 1969;132(2):235–44.
2. Emerson et al. Frequentist evaluation of group sequential clinical trial designs. Stat Med. 2007;26:5047–80.
3. Whitehead. The design and analysis of sequential clinical trials. John Wiley & Sons Ltd. 2000.
4. Jennison et al. Group sequential methods with applications to clinical trials. Chapman & Hall/CRC. 2000.
5. Gillen et al. Designing , monitoring , and analyzing group sequential clinical trials using the “RCTdesign” Package for R. 2012.
6. Rudser et al. Implementing type I & type II error spending for two-sided group sequential designs. Contemp Clin Trials. 2008;29(3):351–8.
7. Kittelson et al. A unifying family of group sequential test designs. Biometrics. 1999;55:874–82.
8. Whitehead. A unified theory for sequential clinical trials. Stat Med. 1999;18(17–18):2271–86.
9. Hwang et al. Group sequential designs using a family of type I error probability spending functions. Stat Med. 1990;9(12):1439–45.
10. Stallard et al. Comparison of Bayesian and frequentist group-sequential clinical trial designs. BMC Med Res Methodol. 2020;20(1):4.
11. Gerber et al. gsbDesign: An R package for evaluating the operating characteristics of a group sequential Bayesian design. J Stat Softw. 2016;69(11):1–23.
12. Zhao. Frequentist and Bayesian interim analysis in clinical trials: Group sequential testing and posterior predictive probability monitoring using SAS. 2016.
13. Lewis et al. Sequential clinical trials in emergency medicine. Ann Emerg Med. 1990;19(9):1047–53.
14. Tamhane et al. A gatekeeping procedure to test a primary and a secondary endpoint in a group sequential design with multiple interim looks. Biometrics. 2018;74(1):40–8.
15. Pocock. When (not) to stop a clinical trial for benefit. JAMA. 2005;294(17):2228–30.
16. Todd et al. Interim analyses and sequential designs in phase III studies. Br J Clin Pharmacol. 2001;51(5):394–9.
17. Whitehead. Group sequential trials revisited: Simple implementation using SAS. Stat Methods Med Res. 2011;20(6):635–56.

Choosing stopping boundaries or rules and the timing and frequency of interim analyses

There is always a tension between the desire to stop the trial early and the need to provide robust evidence to safeguard future patients from sensational but premature conclusions about effects of a new treatment, which may turn out to be wrong had the trial continued. A balance is often made by selecting more stringent stopping boundaries (thresholds) at earlier interim analyses, which become less liberal later on 1 . Thus, researchers penalise themselves by raising the bar of evidence required to stop early very early on in the trial too high (i.e., to require very strong or overwhelming evidence). However, how stringent one needs to be depends on the research context at hand. For example, researchers and the society may be willing to take a risk to accept less stringent stopping boundaries in a trial investigating a new treatment for a fatal or life-threatening medical condition, especially where this affects many people and there is no currently available treatment (COVID19 being a very obvious recent example). Researchers should decide on whether they require the same level of evidence to stop early for efficacy or futility in a trial (in both directions in favour or against the new treatment): symmetric boundaries 2, 3 are relevant when this is the case – otherwise, they should consider asymmetric boundaries 4, 5. The RATPAC example under “Practical example illustrating the design, monitoring, and analysis” illustrates the use of asymmetric stopping boundaries. 

Researchers also need to decide whether group sequential tests should be two-sided or one-sided depending on the research context and how the primary hypothesis is structured (see 3 slides 72-73). For example, in a one-sided group sequential test, researchers are not interested in demonstrating that the comparator is better than the new treatment so the trial is designed without early stopping options for futility or efficacy of the comparator (e.g., a placebo). On the other hand, for instance, when investigating a new treatment that is already being used in practice without evidence against an active comparator (e.g. routine care), researchers may be interested in demonstrating whether the new treatment is better than the comparator or vice versa. Also, researchers should decide which stopping boundaries can be overruled or ignored during interim analyses without affecting the preset threshold for making false-positive claims (non-binding rules) and binding rules which cannot be ignored or overruled (otherwise the type I error rate cannot be controlled). 

In summary, the choice of stopping boundaries or rules to use depends on the research context (e.g., the medical condition, the treatment being assessed, and available standard of care) balancing the interest of several stakeholders such as patients, regulators, society, and the research community.

PANDA users may wish to read general considerations for related discussions on choosing the timing and frequency of interim analyses. 

References

1. Pocock. Current controversies in data monitoring for clinical trials. Clin Trials. 2006;3(6):513–21.
2. Emerson et al. Frequentist evaluation of group sequential clinical trial designs. Stat Med. 2007;26:5047–80.
3. Gillen et al. Introduction to the design and evaluation of group sequential clinical trials. 2016.
4. Todd et al. Interim analyses and sequential designs in phase III studies. Br J Clin Pharmacol. 2001;51(5):394–9.
5. Whitehead. The design and analysis of sequential clinical trials. John Wiley & Sons Ltd. 2000.

How interim decisions are made?

Interim analyses are there to help researchers decide whether a trial should be stopped early because there is already sufficient evidence or to continue because results are inconclusive and more data are required.  At an interim analysis, outcome data are analysed using a statistical model appropriate in that context (e.g., logistic or linear regression model) during hypothesis testing to obtain a measure of treatment effect that matches how the pre-specified stopping boundaries were presented (e.g., mean difference, the posterior probability of the mean difference being greater than a certain value, p-value, etc) (see 1). This treatment effect measure is compared with the corresponding preset stopping boundary and if it crosses this boundary, researchers stop the trial to claim that sufficient evidence has been gathered to make a conclusion consistent with the region where the treatment effect measure falls. 

Ideally, interim analyses should be performed and recommendations to stop the trial made by those not involved in the trial conduct to minimise the potential of introducing operational bias (see general considerations).

PANDA users may wish to read more on the discussion and complex issues that may arise when stopping a trial early with examples 2, 3, 4, 5, 6. 

References

1. Todd et al. Interim analyses and sequential designs in phase III studies. Br J Clin Pharmacol. 2001;51(5):394–9
2. Pocock. Current controversies in data monitoring for clinical trials. Clin Trials. 2006;3(6):513–21.
3. Grant et al. Issues in data monitoring and interim analysis of trials. Health Technol Assess. 2005;9(7):1–238.
4. Pocock et al. Trials stopped early: Too good to be true? Lancet. 1999;353(9157):943–4.
5. Pocock et al. The data monitoring experience in the Candesartan in Heart Failure Assessment of Reduction in Mortality and morbidity (CHARM) program. Am Heart J. 2005;149(5):939–43.
6. Zannad et al. When to stop a clinical trial early for benefit: Lessons learned and future approaches. Circ Hear Fail. 2012;5:294–302. 

Ethics considerations

Group sequential trials by their nature are ethically advantageous. However, they may raise other ethical issues that researchers should think about (see 1, 2, 3 for a detailed discussion). First, interim data for decision-making should be sufficient to make robust decisions – otherwise, the risks of making incorrect conclusions about the benefits and harms of a new treatment are high. Trials that stop early may not collect enough information on possible harms, thereby allowing potentially unsafe treatments to be wrongly recommended for use harming many future patients.

Second, researchers should think about the implications of early stopping decisions on the clinical management of trial patients. For example, how will the patients in the comparator already treated with an effective treatment or those that were randomised to receive the new treatment but waiting treatment be treated after early stopping and who will be responsible for their care? For the latter, to lessen the problem interim analysis should be done and recommended decisions communicated quickly to relevant parties and in some cases, the trial is paused depending on the pace of recruitment.

PANDA users may wish to read more on other ethical considerations that apply to other adaptive trials (see general considerations). 

References

 1. Zannad et al. When to stop a clinical trial early for benefit: Lessons learned and future approaches. Circ Hear Fail. 2012;5:294–302.
2. Mueller et al. Ethical issues in stopping randomized trials early because of apparent benefit. Ann Intern Med. 2007;146(12):878–81.
3. Deichmann et al. Bioethics in practice: Considerations for stopping a clinical trial early. Ochsner J. 2016;16(3):197–8.

Tips on explaining the design to stakeholders

 Researchers should explain why early stopping of a trial is essential in the context of the research question and medical condition, which could include potential ethical, financial or time-saving benefits. There should be a compelling ethical concern and convincing statistical evidence, especially when considering early stopping for efficacy, for results to influence practice while balancing the interests of individual patients within the trial (individual ethics) and future patients outside the trial (collective ethics). 

Like any other adaptive design, the group sequential trial should be logistically feasible to implement, and the decision-making criteria should be justified to reassure stakeholders that the results will influence clinical practice. 

Finally, researchers should communicate the performance of the GSD to reassure its appropriateness to address research questions. For instance, describing the chances of stopping early for a considered criterion (e.g., futility or efficacy) under different assumptions of the true treatment effect, including the risk that GSDs in some cases prolongs rather than shortens recruitment.

Practical example to illustrate the design, monitoring, and analysis

There are some additional examples in the literature with code to illustrate implementation 1, 2 which may be of interest to PANDA users. 

RATPAC 3 retrospective trial 

Here, we redesign the RATPAC trial (introduced in “can we do better”) using a GSD, perform interim analyses and apply stopping rules, and conduct appropriate inference. This is in an emergency care setting and the primary outcome is quickly observed which is appealing for an adaptive design 4. 

1) Design

The primary outcome was the proportion of patients successfully discharged home after Emergency Department (ED) assessment, defined as patients who had (i) either left the hospital or were awaiting transport home with a discharge decision having been made at 4 hours after initial presentation and (ii) suffered no major adverse event during the following 3 months. Researchers assumed a 50% standard of care hospital discharge rate and a 5% increase was deemed clinically relevant for the point of care intervention to be adopted in practice. For a fixed trial design (only one analysis at the end), a total of 3130 (1565 per arm) patients were required to achieve a power of 80% for a 5% two-sided type I error rate without continuity correction. 

Let us assume researchers wanted to incorporate interim analyses, which allow the trial to stop for one of two reasons:

  • futility – where the point of care shows minimal or no difference on interim analysis, 
  • efficacy – overwhelming effect of point of care. 
Here, it is logical to consider asymmetric stopping boundaries, since we require different levels of evidence for early stopping for futility and efficacy. That is, we want to set a very high bar for efficacy such that if stopping happens, evidence will be unequivocal to change practice. On the other hand, we want lower evidence for futility since if the interim effect is in the wrong direction, it is extremely unlikely to change direction after interim analysis and cross the efficacy boundary in the end. We may make stopping rules binding (in which we must stop once a boundary is reached) or non-binding (in which stopping is optional). Non-binding rules are more flexible and allow continuation if other aspects (in particular costs or safety) are not addressed by the (interim) primary analysis, and for now, we consider a non-binding futility boundary to offer more flexibility as this can be overruled without undermining the validity of the design and results. Thus, the computation of the efficacy boundaries assumes the trial continues even when the futility boundary is crossed. 

We illustrate a GSD with two interim analyses to be undertaken after:

    i) 50% of the total number have outcome data and, 
    ii) 70% of the total number have outcome data. 

These percentages are not the only possible choices – in principle, an infinite number could be used, and it makes sense to look at different options but we will use these to illustrate its application. In practice, one may need to compare the performance of competing GSDs. 

Since the standard of care was already the first choice in practice, we may not be interested in finding out whether it is superior to point of care, rather whether the point of care improves upon the standard of care. We will, therefore, consider an asymmetric two-sided GSD with 80% power and 2.5% one-sided type I error. We use a more stringent efficacy stopping boundary and less conservative non-binding futility boundary. For illustration, this is achieved by using a Hwang-Shih-DeCani alpha spending function 5 with a gamma of -7 and a corresponding beta spending function with a gamma of -2. We will present these stopping boundaries on different scales that can be easily understood by different stakeholders. We use R packages “gsDesign” and “rpact” for quality assurance as they produce similar results.

References

1. Gillen et al. Designing , monitoring , and analyzing group sequential clinical trials using the “RCTdesign” package for R. 2012.
2. Gillen et al. Introduction to the design and evaluation of group sequential clinical trials. 2016.
3. Goodacre et al. The Randomised Assessment of Treatment using Panel Assay of Cardiac Markers (RATPAC) trial: a randomised controlled trial of point-of-care cardiac markers in the emergency department. Heart. 2011;97(3):190–6. 
4. Flight et al. Can emergency medicine research benefit from adaptive design clinical trials? Emerg Med J. 2016;emermed-2016-206046.
5. Hwang et al. Group sequential designs using a family of type I error probability spending functions. Stat Med. 1990;9(12):1439–45.
Code
# fixed sample size design without continuity correction is approx. 3130 (1565 per arm)

R code: 
nfx<-nBinomial(p1=0.50, p2=0.55, alpha = 0.025, beta = 0.2, delta0 = 0, scale = "Difference") 
nfx

Stata code: 
sampsi 0.50 0.55, power(0.8) nocont alpha(0.05)
  

R code using gsDesign()

#install and load package 
install.packages(“gsDesign”) 
library(gsDesign)

#fixed sample size  
nfx<-nBinomial(p1=0.5, p2=0.55, alpha = 0.025, beta = 0.2, delta0 = 0, scale = "Difference")

# set a vector indicating  when interim analysis will happen relative to maximum sample size (information fraction) 
analysis_time<-c(0.5, 0.70, 1)

# derive the group sequential design 
design1<-gsDesign(k=3, test.type=4, alpha=0.025, beta=0.2, astar=0,
         timing=analysis_time, sfu=sfHSD, sfupar=c(-7), sfl=sfHSD, sflpar=c(-2), 
         tol=0.000001, r=80, endpoint="binomial", n.fix = nfx, delta1=-0.05, delta0=0, 
         delta = 0, overrun=0 
         ) 

# a summary note of the design and details 
summary(design1) 
design1

# a summary of efficacy and futility boundaries at each analysis on z, p-value and difference in proportion scales 
# note parameterisation of treatment effect in the results is soc-poc rather than poc-soc  
bsm<-gsBoundSummary(design1, digits = 4) 
bsm

# a function to calculate repeated confidence intervals 
gsBinRCI<-function(d, x1, x2, n1, n2){ 
        y<-NULL   
        rname<-NULL
        nanal<-length(x1)
        for (i in 1:nanal) { 
               y<-c(y, ciBinomial(x1 = x1[i], x2 = x2[i], n1=n1[i], n2 = n2[i], alpha = 2*pnorm(-d$upper$bound[i])))     
               rname<-c(rname, paste("Interim analysis", i))   
              }   
        ci<-matrix(y, nrow = nanal, ncol = 2, byrow = T) 
        rownames(ci)<-rname  
        colnames(ci)<-c("LCI", "UCI")
        ci 
       } 

# observed data and events at the first interim analysis (n=1659) 
n1<-c(833) 
n2<-c(826) 
events1 <-c(254) 
events2 <-c(119)
  
# compute repeated intervals using the above function 
rci<-gsBinRCI(design1, events1, events2, n1, n2) 
rci
 
# observed events and MLE of the difference in rates 
p1<-round(events1/n1, 3) 
p2<-round(events2/n2, 3) 
propdif<- round(events1/n1 - events2/n2, 3) 
p1 
p2 
propdif
  

R code using rpact()

# installing and loading package 
install.packages(“rpact”) 
library(rpact) 

# set up the group sequential design 
ratdesign<-getDesignGroupSequential( 
    kMax = 3, alpha = 0.025, 
    beta = 0.2, sided = 1, informationRates = c(0.5, 0.7, 1), 
    typeOfDesign = "asHSD", gammaA = -7, typeBetaSpending = "bsHSD", gammaB = -2, 
    bindingFutility = FALSE, twoSidedPower = FALSE 
  ) 
ratdesign 

# get the sample sizes of the above design we set up (at each interim and maximum) 
ratpac1<-getSampleSizeRates( 
    design=ratdesign, groups = 2, thetaH0 = 0.00, pi1=0.55, pi2=0.5, 
    normalApproximation = TRUE 
  ) 
summary(ratpac1) 

# first interim analysis when 1659 patients were recruited 
# input data and observed events in each arm 

ratpacdata<-getDataset( 
  n1 = c(833), n2 = c(826), 
  events1 = c(254), events2 = c(119) 
  ) 

interim1res<-getAnalysisResults(ratdesign, ratpacdata) 
interim1res 

# action to take given the results and corresponding stopping boundaries 
getTestActions(ratdesign, stageresults) 

# produce the final results 
getFinalConfidenceInterval(ratdesign, ratpacdata) 

# get stage results first, and final overall p-value 
stageresults<-getStageResults(ratdesign, ratpacdata, stage=1) 
stageresults 
getFinalPValue(ratdesign, stageresults)

2) Stopping boundaries 

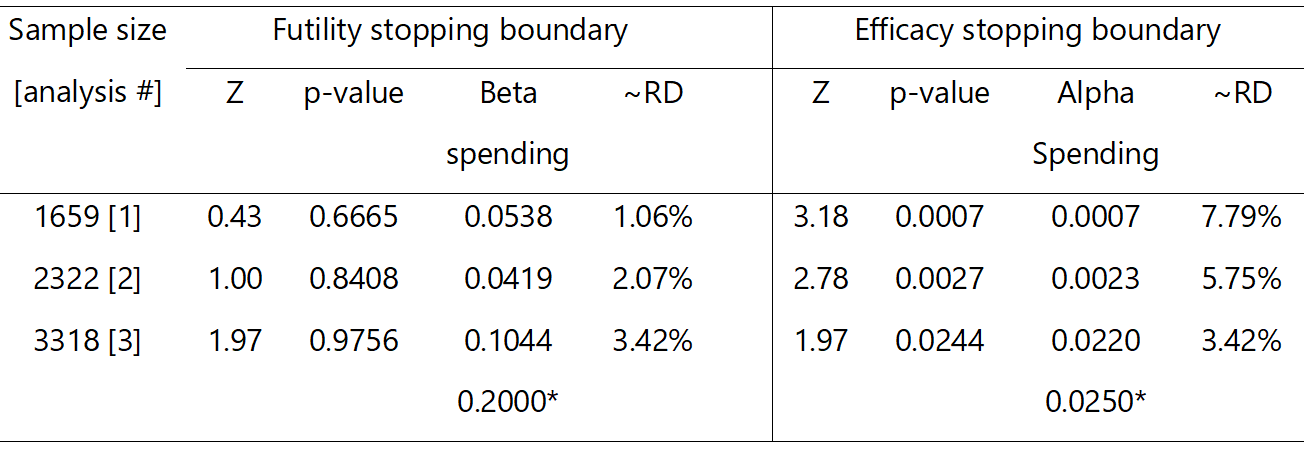
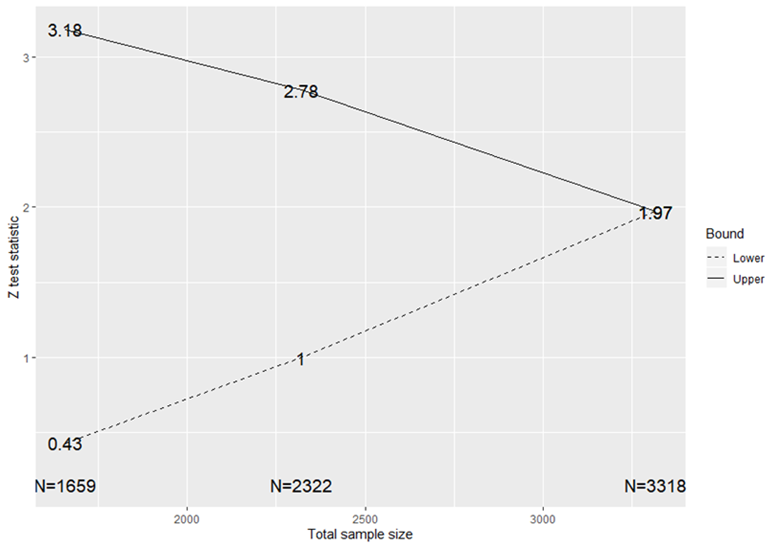
Table 1 summarises the efficacy and futility stopping boundaries on different scales corresponding to each interim analysis including how evidence is claimed at the final analysis. The information on the Z test statistic and risk difference scales are displayed in Figure 3 and Figure 5, respectively. For instance, at the first interim analysis after recruiting 1659 (~830 per arm), we will stop for futility if the point of care improved hospital discharge by any amount less than 1.06% absolute difference (equivalent to a Z test statistic of 0.43). On the other hand, at this interim analysis, we will stop to claim efficacy if the point of care resulted in more than 7.79% absolute improvement in hospital discharge (equivalent to a Z test statistic of 3.18). As can be seen, the overall type I and II errors at the end of the study are 2.5% and 20% as desired, respectively. 

Table 1.

Table 1. RATPAC stopping boundaries. RD, risk difference (point of care – standard of care); * total error spend at the end of the study assuming no stopping; Z, standardised Z test statistic; p-values are one-sided

RATPAC stopping boundaries. RD, risk difference (point of care – standard of care); * total error spend at the end of the study assuming no stopping; Z, standardised Z test statistic; p-values are one-sided.

Figure 3.

Figure 3. Stopping boundaries for a RATPAC group sequential test

Stopping boundaries for a RATPAC group sequential test

 3) Performance of the design

To assess the performance of the design, we should ask ourselves the following questions depending on the scope of early stopping considered:

  • are the chances of stopping for futility reasonable or meet our expectations when we know that the study treatment is futile? 
  • is the evidence convincing enough to justify early stopping? 
  • are the chances of stopping for efficacy when we know the effect is overwhelmingly good enough for the design to be worthwhile? 
  • do the benefits of the design justify its use against additional logistical and practical challenges? 
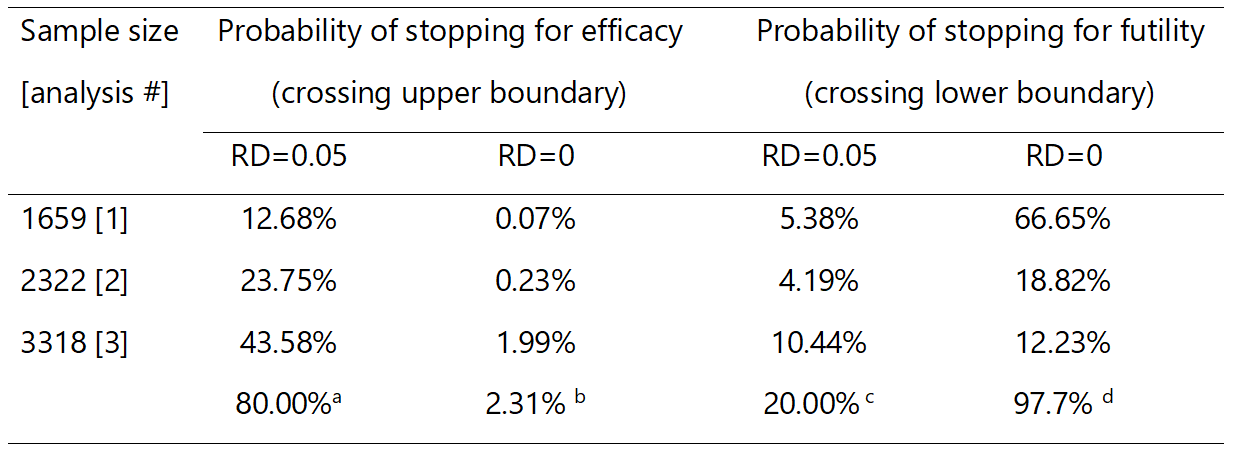
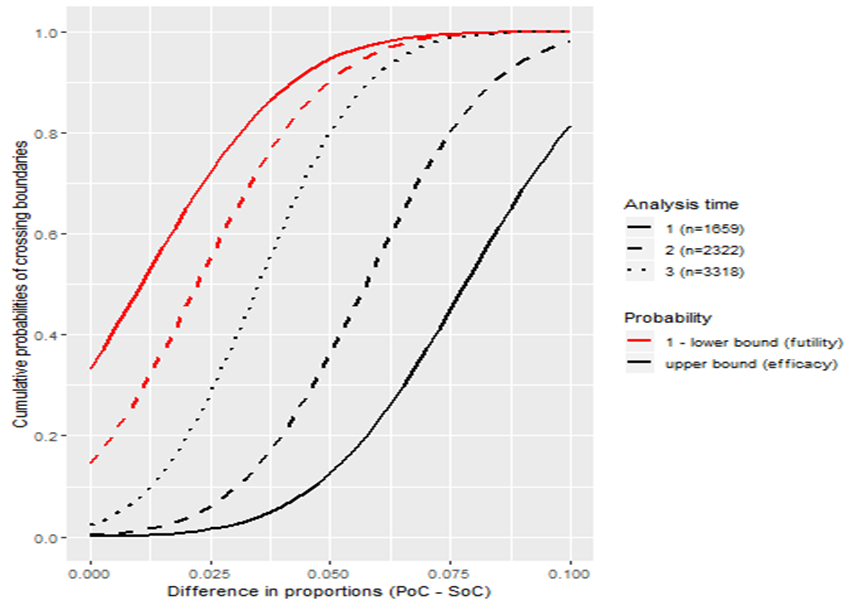
Table 2 presents the probabilities of early stopping for futility or efficacy at each analysis assuming the true treatment effect of no difference or 5% in favour of the point of care. For example, we have a 20% chance of stopping early for efficacy at the first interim analysis if the true treatment effect is 5%. On the other hand, if the true treatment effect is zero, we will have a 67% chance of stopping for futility at the first interim analysis.  

Table 2.

Probabilities of stopping for efficacy and futility assuming effect under the null and alternative hypotheses

Probabilities of stopping for efficacy and futility assuming effect under the null and alternative hypotheses.

a probability of statistical power; b probability of incorrectly concluding that point of care is effective when it is not (type I error); c probability of incorrectly concluding that point of care is ineffective when in fact it is effective (type II error); d probability of correctly concluding that point of care is ineffective (1-type I error); RD, risk difference.

We can explore the performance of the design by varying the treatment effect from 0% to 10% as illustrated in Figure 4. For instance, if the treatment effect is overwhelming, the design will have no chance of stopping for futility but may stop for efficacy: the probability of stopping early for efficacy is 58% if the treatment improves discharge rates by 7.5%, and reaches close to 90% for a 10% underlying treatment effect. Figure 4 can be used to assess the performance of competing GSDs to inform the choice of an appropriate better design. 

Figure 4.

Probabilities of stopping for efficacy or futility during the trial assuming different scenarios about the true treatment effect (PoC, point of care; SoC, standard of care)

Probabilities of stopping for efficacy or futility during the trial assuming different scenarios about the true treatment effect (PoC, point of care; SoC, standard of care).

4) Impact and potential benefits 

The maximum sample size we should commit upfront is 3318 (1659 per arm) which is slightly more than a fixed trial design by 188 patients (inflation factor of 1.06). This is the penalty we pay when early stopping opportunities fail to pan out: GSDs inevitably increase the maximum sample size. However, when we account for the chances of stopping at each interim analysis we need fewer participants if the treatment works as we expect it to or if it is ineffective: the GSD allows us to stop earlier whereas fixed trials do not. The saving depends on how effective (or ineffective) the treatment is but on average, we will only need to recruit 2021 if there is no treatment effect or 2740 if the 5% hypothesised treatment effect exists. This is an average saving of 1109 or 400 patients compared to the fixed trial design, respectively. 

There is a downside: if the intervention has a small impact, there are no savings since neither stopping boundary is likely to be crossed before the final analysis is reached. In the RATPAC example there are clear benefits of GSDs where the difference between arms is 0% or 5%, but for more modest differences the GSD requires larger sample size on average than a fixed trial design.   

It is not surprising that the expected sample size savings under the alternative hypothesis are smaller because we used a very stringent efficacy stopping rule. If we stop at the first or second interim analysis, we would have saved a total of 1471 and 808 patients compared to a fixed sample size design, respectively. One could further quantify study duration and financial saving using the expected recruitment rate and cost per patient 1, 2 and balance these against the additional operational costs incurred by a GSD.  

5) First interim analysis results 

Figure 5 displays the observed risk difference with uncertainty throughout the entire trial, the interim results, and the final results after early stopping at the first interim analysis superimposed on the prespecified stopping boundaries (on risk difference scale). Using the data from the first 1659 patients, 826 (standard of care) and 833 (point of care) patients would have been recruited; successful discharge rates were 119 (14.4%) and 254 (30.5%), respectively. This translated to an unadjusted improvement in successful discharge rate attributed to point of care compared to standard of care of 16.1% (95% repeated confidence interval: 9.7% to 22.5%). We now compare this result to the stopping boundaries at the corresponding first interim analysis (Table 1). According to the design, we should stop the trial at this point and claim overwhelming effectiveness of point of care in improving successful hospital discharge rate since the interim effect (risk difference=16.1%; Z=7.847) is far greater than the efficacy stopping boundary (risk difference=7.08%; Z=2.89). Based on the stagewise ordering method, the final median unbiased risk difference is 16.1% (95% confidence interval: 12.1% to 20.0%, p-value<0.00001). The exact p-value is 2.109424 x 10 -15. 

Figure 5.

Monitoring of RATPAC trial

Monitoring of RATPAC trial. MLE, maximum likelihood estimate; RCI, repeated confidence interval; MUE, median unbiased estimate based on stagewise ordering method; CI, confidence interval; IA, interim analysis; FA, final analysis.

The RATPAC trial was stopped after recruiting 2243 patients when funding ran out and the funding extension request was not approved. At this point, successful hospital discharge rates in the standard of care and point of care were 146 (13.1%) and 358 (31.8%), respectively, with an unadjusted risk difference of 18.8% (95% confidence interval: 15.4% to 22.1%; p<0.00001). These results are similar to the first interim results if the trial had been stopped early.

References

 1. Sutton et al. Influence of adaptive analysis on unnecessary patient recruitment: reanalysis of the RATPAC trial. Ann Emerg Med. 2012;60(4):442-8.
2. Dimairo. The Utility of adaptive designs in publicly funded confirmatory trials. University of Sheffield. 2016;page 219.

Tips on planning and implementing group sequential trials

 ❖ Seek the buy-in of stopping rules from key stakeholders (e.g., clinical groups, patient representative groups, and regulators) and agree on upfront as a research team; 

❖  Avoid too many unnecessary interim analyses as the benefits diminish with an increasing number of interim analyses. In practice, most of group sequential trials are planned with either one or two interim analyses and rarely above four 1;  

❖  Avoid undertaking the first interim analysis too early with very little information, which is highly uncertain to make reliable adaptation decisions; 

❖  Consider both statistical and non-statistical aspects when stopping the trial. Statistical rules are guidelines and well-reasoned considerations beyond stopping rules including clinical aspects and other relevant trial data should be considered during interim decision-making (see 2); 

❖  Consider non-binding futility stopping boundaries if possible to cope with unexpected circumstances that may necessitate overruling of the boundaries without undermining the validity of the design; 

❖  The choice of whether the design should be symmetric is trial dependent and driven by the research question. For instance, if we are comparing two interventions which are already used in practice (but with little evidence), then it could be of interest to know whether either treatment is better than the other, in which case a symmetric design is well-suited; 

❖  Chances of the results crossing future stopping boundaries, given possible interim results when assumptions about future data are made, may provide useful supplementary information to aid interim decision-making. 

References

1. Stevely et al. An investigation of the shortcomings of the CONSORT 2010 statement for the reporting of group sequential randomised controlled trials: A methodological systematic review. PLoS One. 2015;10(11):e0141104.
2. Zannad et al. When to stop a clinical trial early for benefit: Lessons learned and future approaches. Circ Hear Fail. 2012;5:294–302.

Some challenges and limitations

Researchers should be aware of other implications of stopping the trial early (see 1 for a detailed discussion with examples). For example, this will result in fewer outcome data relating to safety, other important secondary clinical outcomes (in some cases) and health economics evaluation. This may be concerning when a trial is stopped because of overwhelming evidence of efficacy since these additional data may be required to support the adoption of the treatment in practice. Potential reversal of the treatment effect after early stopping could be raised in some cases, for example, if interim analysis only covered some seasonal periods believed to favour the new treatment. Researchers need to think carefully about the practical as well as statistical implications of GSDs, and whether a trial that stops early has answered the basic research questions well enough.  

GSDs are often derived based on a single primary outcome and the validity of methods depends on adhering to the planned stopping rules. That is, if the stopping boundary is crossed, then the trial should be stopped accordingly. However, the interim decision-making process is often complicated and involves looking at the totality of evidence from within the trial and external information for reasons that cannot be foreseen. Thus, in some cases, decision rules may be ignored or overruled for compelling reasons although this may complicate the interpretation of trial results. 

Group sequential trials by their nature are often difficult to completely mask researchers and stop them from speculating about the direction of the interim effect merely as a result of interim decisions. This may influence potential operational bias in the conduct of the trial going forward. The extent of this problem is difficult to quantify. Some limitations and challenges that may affect other adaptive trials are discussed in general considerations. 

References

 1. Zannad et al. When to stop a clinical trial early for benefit: Lessons learned and future approaches. Circ Hear Fail. 2012;5:294–302. 

Costing of group sequential trials

On average, a group sequential trial will reduce the sample size if the treatment works as expected since the trial will usually stop earlier than a fixed sample size design that has no without interim analysis. However, a group sequential trial requires a larger sample size than a fixed design if no early stopping happens. Researchers should, therefore, be prepared to recruit this maximum sample size and agree with the funders upfront. Researchers can cost scenarios assuming the trial is stopped at each planned interim analysis including the maximum sample size (assuming no early stopping). Ideally, these costs should be communicated to the funder in a grant application and agree on how the funds saved in the case of early stopping will be spent.

PANDA users may wish to read more on general considerations when costing of adaptive trials.