Multi-Arm Multi-Stage (MAMS)

Planning and design

Appropriateness

MAMS trials are suitable where several candidate treatments (e.g., different drugs, drug combinations, or varying doses/schedules of the same treatment) are available for testing and there is equipoise amongst various parties (e.g., investigators, the wider scientific community, or patients) about which of the treatment options is likely best. 

It is important to balance these advantages against possible disadvantages. MAMS trials are difficult to conduct when some study participants express a strong preference for some treatments over others and would not consider (or be suitable for) all of the treatment options being evaluated. To illustrate this with an example, a patient may be willing to undergo randomisation between different therapeutic options, but may be unwilling to consider (or ineligible for) surgical options. A trial which incorporates both medical and surgical options may therefore suffer from having too few patients from which to recruit. In a similar vein, the caregiver may have their own opinions on which treatments they are willing to randomise a patient to (i.e., lack equipoise), again limiting the ability to recruit. Lastly, the sponsors may be unwilling to conduct a head-to-head comparison of their own treatments to those involving their competitors because of commercial interests (limiting interventions available for testing). To some extent, these considerations apply to all trials, but apply more obviously to multi-arm designs.

Some considerations that apply to every trial with one or more interim analyses are also relevant here (see general considerations).

Design concepts

In MAMS trials, we start with multiple treatment candidates to be investigated against shared comparator(s). At the design stage, we decide on:

  • the primary outcome for the interim and final analyses - note that the outcome to be used at interim analyses (adaptation outcome) may differ from the final analysis outcome (see statistical methods);
  • how evidence of a treatment effect is declared (e.g., statistical significance);
  • when and how often interim analyses are performed;
  • the treatment selection rule (how promising treatments are selected for further testing or poorly performing treatments are dropped) including stopping criteria (e.g., when the entire trial is stopped);
  • the desired statistical properties to be controlled (e.g. familywise or pairwise type I error rate, overall or stagewise power);
  • the statistical method to control the desired statistical properties (see statistical methods);
  • how patients are allocated to treatments.
We can then determine the maximum sample size needed for the entire study, including the sample sizes for each treatment group at each interim analysis. Participants are randomised to receive one of the treatments and followed up to assess their outcomes. 

At each interim analysis, when the required number of participants with observed outcome measurements have been recorded, we analyse outcome data, and decisions are made given the observed interim treatment effects and the treatment selection and stopping rules. If the trial is not stopped entirely, the trial proceeds with the selected treatment arms to the next stage, which could be another interim analysis (for which this process is repeated), or the final analysis.

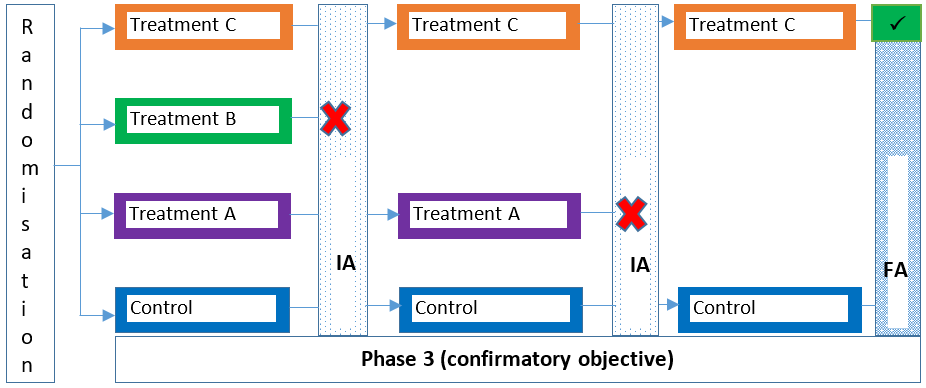
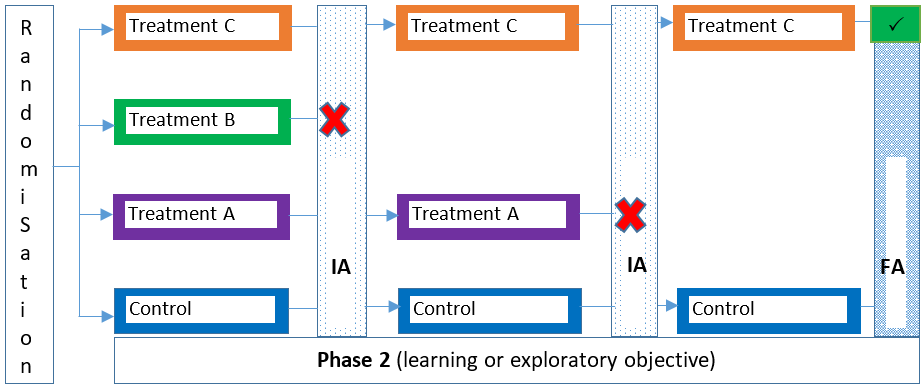
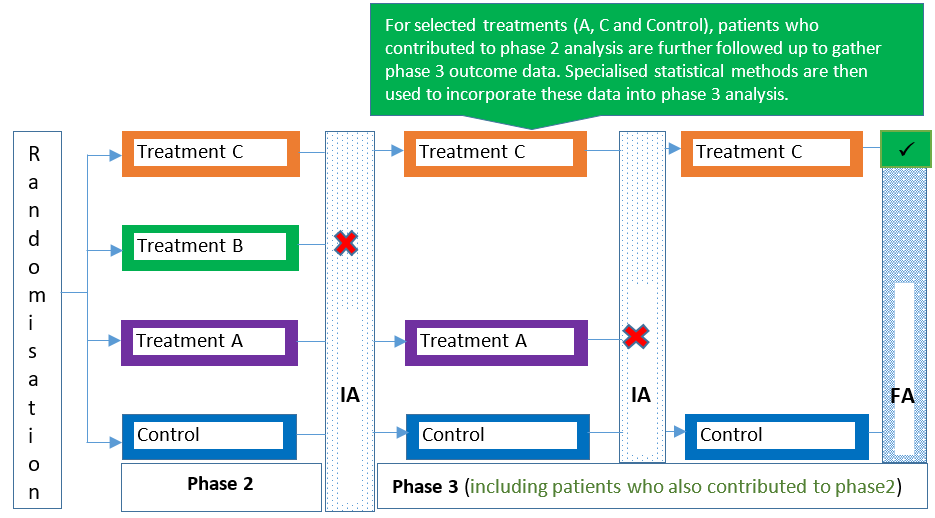
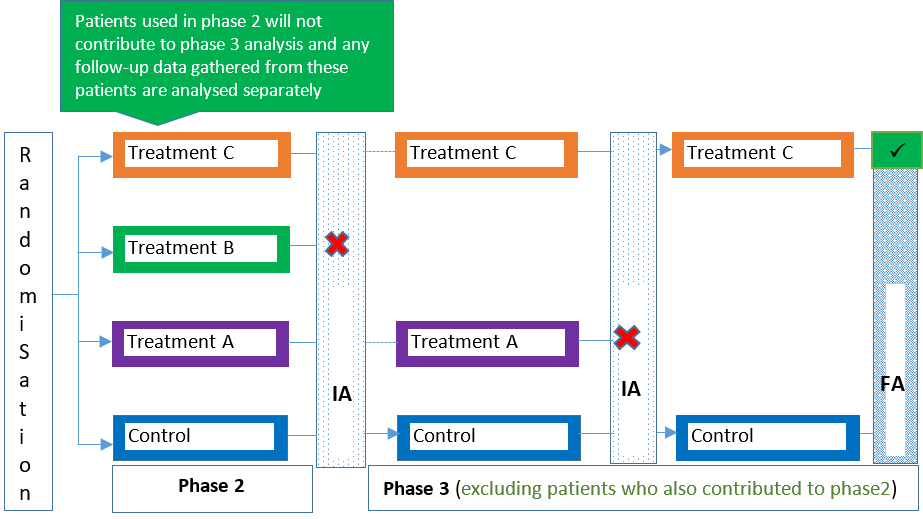
Trial phases covered by MAMS designs

Traditional clinical trials are typically categorised as either a phase 1, 2, 3 or 4 trial depending on the stage of the intervention’s development and research goals/objectives. MAMS designs can be used in the same way in these trial phases (e.g., see 1, 2), but can also span more than one trial phase (e.g., see 3, 4, 5) as a seamless design. For example, a seamless phase 2/3 trial combines more exploratory (learning) and confirmatory objectives in a single trial. Figures 1-4 illustrate some variants of the MAMS design.

Figure 1.

Phase 3 MAMS design (IA, interim analysis; FA, final analysis)

Phase 3 MAMS design (IA, interim analysis; FA, final analysis).

Figure 2.

Phase 2 MAMS design (IA, interim analysis; FA, final analysis)

Phase 2 MAMS design (IA, interim analysis; FA, final analysis).

Figure 3.

Inferential seamless phase 2/3 MAMS design (IA, interim analysis; FA, final analysis).

Inferential seamless phase 2/3 MAMS design (IA, interim analysis; FA, final analysis).

Figure 4.

Operational seamless phase 2/3 MAMS design (IA, interim analysis; FA, final analysis).

Operational seamless phase 2/3 MAMS design (IA, interim analysis; FA, final analysis).

References

1. Pushpakom et al. TAILoR (TelmisArtan and InsuLin Resistance in Human Immunodeficiency Virus [HIV]): An adaptive- design, dose-ranging phase IIb randomized trial of telmisartan for the reduction of insulin resistance in HIV-positive individuals on combination antiretroviral. Clin Infect Dis.  2019 ; 70: 2062–2072.
2. Pushpakom et al. Telmisartan to reduce insulin resistance in HIV-positive individuals on combination antiretroviral therapy: the TAILoR dose-ranging Phase II RCT. Effic Mech  Eval. 2019; 6: 1–168.
3. Donohue et al. Once-daily bronchodilators for chronic obstructive pulmonary disease: indacaterol versus tiotropium. Am J Respir Crit Care Med. 2010; 182: 155–62.
4. Barnes et al. Integrating indacaterol dose selection in a clinical study in COPD using an adaptive seamless design. Pulm Pharmacol Ther. 2010; 23: 165–71.
5. Brown et al. Multiple interventions for Diabetic Foot Ulcer Treatment Trial (MIDFUT): Study protocol for a randomised controlled trial. BMJ Open. 2020;10(4):e035947. 

Prospective case studies

The number of MAMS trials being conducted in practice is steadily increasing 1 (e.g., see 2, 3, 4, 5, 6). We illustrate these trials with two recent examples.

1. TAILoR trial 2, 7  

TAILoR was a phase 2 study investigating the efficacy of Telmisartan, a licensed treatment in hypertension, for treating insulin resistance in HIV positive patients on antiretroviral therapy. It compared three different doses of Telmisartan (20 mg, 40 mg, and 80 mg) to control (no intervention) using the change in insulin resistance as measured by the HOMA-IR score as the primary endpoint, which was assumed to be normally distributed. When designing the trial, the researchers targeted a standardised effect size of 0.545 in order to declare any dose of Telmisartan efficacious compared to the control. See additional information on the design under “examples of how MAMS trials are designed”.

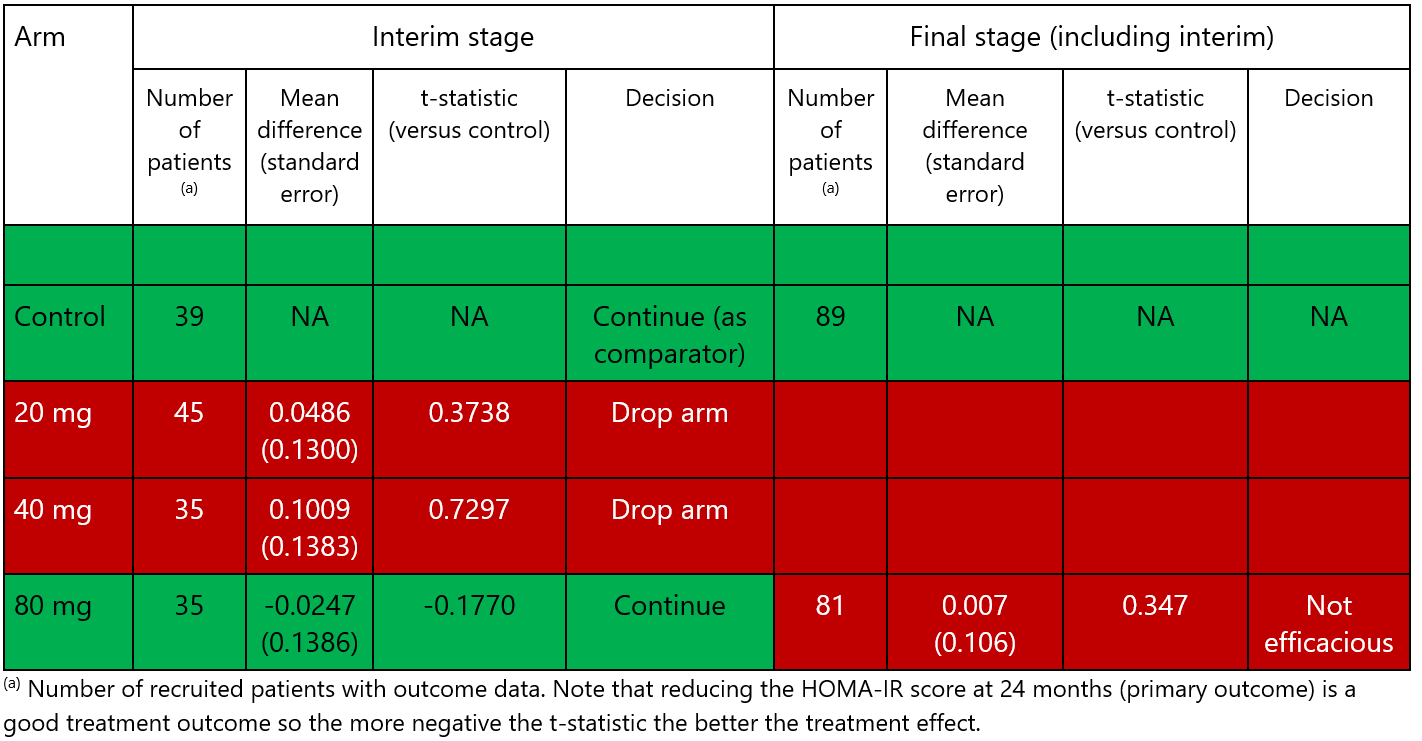
A single interim analysis was undertaken once at least 42 patients per arm had primary outcome data recorded. The possible decisions were:

  • stop the study because of overwhelming efficacy from at least one of the doses;
  • stop the study because none of the doses of Telmisartan was sufficiently promising to warrant further investigation;
  • continue the study, retaining any dose that was deemed promising plus the control arm.
The trial used a liberal definition of “promising” wherein any reduction in mean HOMA-IR compared to the control arm was acceptable. Any dose level that did not meet this criterion was dropped at the interim analysis. If the study was not stopped for futility or efficacy, promising doses of Telmisartan were continued in the second stage of the study and included in the final analysis where an efficacy comparison versus control was to be made. The study used a generalisation of the Dunnett test 8 to ensure that the overall type I error (familywise error rate) was controlled at a 5% one-sided level.

At the interim analysis (see Table 1), two doses (20 mg and 40 mg) were dropped; the point estimate for reduction in mean HOMA-IR was less than that seen in the control arm. Only the 80 mg dose showed sufficiently promising improvement in HOMA-IR compared to the control and so was carried forward to stage 2. At the final analysis, the 80 mg dose did not show significant clinical improvement in HOMA-IR 2.  Thus, the study did not find any of the doses to be significantly better than control. The adaptive nature of the trial meant two of the doses were dropped from the study at the interim analysis; therefore, 84 patients (42 on each arm) did not need to be recruited for the second stage. In addition, multiple research questions were addressed in a single trial.

Table 1.

Table 1. Interim and final results with decisions made.

Interim and final results with decisions made.

 2. PANACEA MAMS-TB trial 5 

The PANACEA-MAMS-TB trial compared four different treatment combinations involving doses of rifampicin, moxifloxacin, or SQ109 (RIFQHZ, RIF20QHZ, RIF20MHZ, and RIF35HZE) to a shared control arm. The control arm received a standard dose of rifampicin, isoniazid, pyrazinamide, and ethambutol for 8 weeks followed by a standard dose of rifampicin and isoniazid for 18 weeks. The primary endpoint was time to culture conversion in liquid media within 12 weeks. Researchers assumed an 85% culture conversion rate at 12 weeks in the shared control arm and 5% loss to follow-up. Two interim analyses were planned at which arms could be dropped if they were insufficiently promising, but no early stopping for efficacy was allowed. The design was constructed so that the pairwise two-sided type I error rate was controlled at 5% and the pairwise power was 90% for a targeted hazard ratio (HR) of 1.8 (indicating an 80% relative increase in culture conversion rate compared to control). At each interim analysis, there was a 95% chance of continuing an efficacious arm (i.e., 95% stagewise power), and 40% and 20% chance of not dropping an inefficacious arm at the first and second interim analyses (i.e., stagewise type I error rates), respectively. Treatment arms were to be terminated if they showed a HR less than 1.09 (first interim) or less than 1.23 (second interim) compared to the shared control. The trial required a maximum of 372 participants (124 in the control and 62 in each experimental treatment arm). The two interim analyses were planned after 28 and then 50 participants in the control arm had achieved stable culture conversion. 

Two of the arms (RIFQHZ and RIF20QHZ) were dropped at the first interim analysis due to insufficient promise and hence a reduction in the maximum sample size was achieved. The second planned interim analysis was not performed as all patients had already been recruited by the time it should have taken place. At the final analysis, it was found that one combination arm (RIF35HZE) was significantly better than control, while no difference was found for the other RIF20MHZ arm.

References

1. Bothwell et al. Adaptive design clinical trials: a review of the literature and ClinicalTrials.gov. BMJ Open. 2018; 8(2):e018320.
2. Pushpakom et al. TAILoR (TelmisArtan and InsuLin Resistance in Human Immunodeficiency Virus [HIV]): An adaptive design, dose-ranging phase IIb randomized trial of telmisartan for the reduction of insulin resistance in HIV-positive individuals on combination antiretroviral. Clin Infect Dis. 2019 Jul 3;70(10):2062–2072.
3. Donohue et al. Once-daily bronchodilators for chronic obstructive pulmonary disease: indacaterol versus tiotropium. Am J Respir Crit Care Med. 2010;182(2):155–62.
4. Cuffe et al. When is a seamless study desirable? Case studies from different pharmaceutical sponsors. Pharm Stat. 2014;13(4):229–37.
5. Boeree et al. High-dose rifampicin, moxifloxacin, and SQ109 for treating tuberculosis: a multi-arm, multi-stage randomised controlled trial. Lancet Infect Dis. 2017;17(1):39–49.
6. Léauté-Labrèze et al. A randomized, controlled trial of oral propranolol in infantile hemangioma. N Engl J Med. 2015;372(8):735–46.
7. Pushpakom et al. Telmisartan to reduce insulin resistance in HIV-positive individuals on combination antiretroviral therapy: the TAILoR dose-ranging Phase II RCT. Effic Mech Eval. 2019;6(6):1–168.
8. Magirr et al. A generalized Dunnett test for multi-arm multi-stage clinical studies with treatment selection. Biometrika. 2012;99(2):494–501. 

Underpinning statistical methods

From a statistical point of view, the main challenges arising in MAMS trials are accounting for the multiple hypothesis tests that are undertaken and determining the selection process of treatments. If the trial is not designed correctly, the risks of erroneously dropping a promising treatment or carrying forward a futile treatment are increased, as is the risk of making incorrect conclusions at the end of the trial (e.g., claiming benefit of treatments when this is not true). Thus, one may want to control the familywise error rate (see 1, 2, 3 for a discussion on when this may be necessary). Several specialised methods with different treatment selection rules have been developed to address these issues on the basis of:

  • normally distributed endpoints 4, 5, 6, 7, 8, 9, 27; 
  • binary endpoints 10, 11, 12, 13, 26; 
  • ordinal endpoints 14, and;
  • time-to-event endpoints 12, 15, 16. 
Some of these methods are based on constructing a measure of treatment effect for each treatment comparison at each interim analysis conditional on all outcome data accumulated prior to that stage (cumulative MAMS).  Moreover, methods that allow flexibility in the selection rule and type of endpoint are also available 12, 17. These flexible methods are based on partitioning outcome data with respect to interim analyses the participant contributed to (such that data for each stage become independent of each other). Outcome data from these independent stages are then analysed separately and results pooled together using a prespecified combination method to produce a measure of treatment effect for adaptation decisions 17. Decision-making will also take into account the prespecified method for controlling the desired type I error rate across multiple hypothesis tests at interim and final analyses (stagewise MAMS). In general, cumulative MAMS are more efficient and powerful compared to stagewise MAMS (see 17 for discussion). Of note, the need to account for multiple hypothesis tests is not applicable in MAMS designs that use Bayesian methods but specific decision errors apply (e.g., see 18, 19). However, relevant MAMS designs using Bayesian methods are available 13, 28, 29. 

The most crucial aspects of a MAMS design are the selection rules used. In general, each of these is highly context-specific depending on the research goals, but in principle, they can be grouped into the following categories: all-promising, pick the winner, and flexible.

a) All promising

The all-promising selection rule continues the study with any treatment that is sufficiently promising at the interim analysis to warrant further study. One implication of this design is that the sample size is not known in advance but it comes with the benefit that several good treatments can be identified, and further decisions about close contenders can be made at the end of the study.

b) Pick the winner

The pick-the-winner rule pre-specifies how many treatment arms are selected at each interim analysis (often only the best active treatment is taken forward). This has the advantage that the sample size is fixed and typically smaller than for the all-promising selection rule. At the same time, treatments that are close second would not be considered further in this setting, thus increasing the risk of not identifying the treatment which is truly the best. 

c) Flexible

A flexible rule does not predetermine how selection will be made. Instead, it provides guidance rather than fixed rules. In doing so, contextual information (e.g., safety, costs, external circumstances such as emerging evidence) can be used to make the selection decision. This is particularly appealing where there are important features which are not quantified by the primary outcome alone or are difficult to incorporate into a fixed decision rule. The cost of this is that these designs tend to be slightly less efficient than designs with pre-specified rules. Moreover, it is more complex to ensure the integrity of the trial as often investigators and steering groups will want to be involved in the selection process (due to vested conflict of interest). As such, flexible rules are controversial outside an exploratory trial setting. 

Some MAMS designs may include stopping rules at an interim analysis beyond stopping as a consequence of treatment selection (e.g., when no promising treatment exists) 20. For example:

  • the entire trial can be stopped when any of the experimental treatment arms is proven effective against the shared control (referred to as simultaneous stopping rules);
  • study treatment arms that have proven effective at an interim analysis are stopped but the trial continues with the remaining arms including the shared control (referred to as separate stopping rules).
The appropriateness of such stopping rules is influenced by factors such as the severity of the condition, available standard of care, and research goals. It is therefore important for researchers to assess the benefits and risks of a certain stopping rule.

MAMS designs can also use an adaptation outcome for interim analyses (e.g. treatment selection) that is different from the primary outcome used at a later stage (e.g., for confirmatory hypothesis testing at the final analysis). This adaptation outcome is often observed early using a surrogate marker rather than the outcome itself (e.g., progression-free survival or change in tumour size as an early marker of overall survival in oncology studies).  Several methods have been proposed to account for the correlation between the adaptation and primary outcomes 10, 11, 16, 21, 22, 23, 24, 25. It is important to note these methods can only be used where reliable surrogate measures exist. 

References

 1. Wason et al. Some recommendations for multi-arm multi-stage trials. Stat Methods Med Res. 2016;25(2):716–27.
2. Wason et al. Correcting for multiple-testing in multi-arm trials: is it necessary and is it done? Trials. 2014;15:364.
3. Stallard et al. On the need to adjust for multiplicity in confirmatory clinical trials with master protocols. Ann Oncol. 2019;30(4):506–9.
4. Magirr et al. A generalized Dunnett test for multi-arm multi-stage clinical studies with treatment selection. Biometrika. 2012;99(2):494–501.
5. Stallard et al. Sequential designs for phase III clinical trials incorporating treatment selection. Stat Med. 2003;22(5):689–703.
6. Wason et al. A multi-stage drop-the-losers design for multi-arm clinical trials. Stat Methods Med Res. 2017;26(1):508–24.
7. Proschan et al. A modest proposal for dropping poor arms in clinical trials. Stat Med. 2014;33(19):3241–52.
8. Ghosh et al. Design and monitoring of multi-arm multi-stage clinical trials. Biometrics. 2017;73(4):1289–99.
9. Wason et al. Optimal multistage designs for randomised clinical trials with continuous outcomes. Stat Med. 2012;31(4):301–12.
10. Bratton et al. A multi-arm multi-stage clinical trial design for binary outcomes with application to tuberculosis. BMC Med Res Methodol. 2013;13:139.
11. Bratton et al. Design issues and extensions of multi-arm multi-stage clinical trials. University College London. 2015.
12. Jaki et al. Considerations on covariates and endpoints in multi-arm multi-stage clinical trials selecting all promising treatments. Stat Med. 2013;32(7):1150–63.
13. Yu et al. Simulation optimization for Bayesian multi-arm multi-stage clinical trial with binary endpoints. J Biopharm Stat. 2019;29(2):306–17. 
14. Whitehead et al. One- and two-stage design proposals for a Phase II trial comparing three active treatments with control using an ordered categorical endpoint. Stat Med. 2009;28(5):828–47.
15. Royston et al. Novel designs for multi-arm clinical trials with survival outcomes with an application in ovarian cancer. Stat Med. 2003;22(14):2239–56.
16. Bratton et al. Type I error rates of multi-arm multi-stage clinical trials: Strong control and impact of intermediate outcomes. Trials. 2016;17(1):309.
17. Ghosh et al. Adaptive multiarm multistage clinical trials. Stat Med. 2020;39:1084–102.
18. Jacob et al. Evaluation of a multi-arm multi-stage Bayesian design for phase II drug selection trials - An example in hemato-oncology. BMC Med Res Methodol. 2016;16(1):67.
19. Brueckner et al. Performance of different clinical trial designs to evaluate treatments during an epidemic. PLoS One. 2018;13(9).
20. Urach et al. Multi-arm group sequential designs with a simultaneous stopping rule. Stat Med. 2016;35(30):5536–50.
21. Friede et al. Adaptive seamless clinical trials using early outcomes for treatment or subgroup selection: Methods, simulation model and their implementation in R. Biometrical J. 2020;62:1264–83.
22. Friede et al. Designing a seamless phase II/III clinical trial using early outcomes for treatment selection: an application in multiple sclerosis. Stat Med. 2011;30(13):1528–40.
23. Parsons et al. An R package for implementing simulations for seamless phase II/III clinical trials using early outcomes for treatment selection. Comput Stat Data Anal. 2012;56(5):1150–60.
24. Blenkinsop et al. Assessing the impact of efficacy stopping rules on the error rates under the multi-arm multi-stage framework. Clin Trials. 2019;16(2):132–41.
25. Blenkinsop et al. Multiarm, multistage randomized controlled trials with stopping boundaries for efficacy and lack of benefit: An update to nstage. Stata J. 2019;19(4):782–802.
26. Jazić et al. Design and analysis of drop-the-losers studies using binary endpoints in the rare disease setting. J Biopharm Stat. 2021;31(4):507–22.
27. Serra et al. An order restricted multi-arm multi-stage clinical trial design. Stat Med. 2022; ;41(9):1613–26.
28. Karanevich et al. Optimizing sample size allocation and power in a Bayesian two-stage drop-the-losers design. Am Stat. 2021;75:66–75.
29. Bassi et al. Bayesian adaptive decision-theoretic designs for multi-arm multi-stage clinical trials. Stat Methods Med Res. 2021;30:717–30.

How are decision rules defined?

The reader may notice that the chance of incorrectly stopping the trial early for efficacy is often designed to be much smaller (more stringent) than the chance of incorrectly continuing to treat patients at an ineffective arm. This makes sense since overwhelming evidence is required to conclude that one or more treatments are so effective, that the trial can be stopped. This is particularly true when such a decision is based on the relatively small number of patients often analysed at an interim analysis.

By contrast, the decision to drop one or more arms for futility is less straightforward. Thus, the decision to continue a treatment arm will generally use a more liberal rule in which treatments are retained for further study if promising, and dropped only if efficacy can safely be ruled out (with a high degree of confidence).

These decision rules should be discussed at the design stage and agreed upon by the research team (including trial statistician and clinical investigators) and relevant parties where appropriate (e.g., regulators, patients).

Ethical considerations

In principle, MAMS designs are ethically advantageous as they aim to speed up the evaluation process of experimental treatments and minimise the number of study participants that are allocated to poorly performing treatments during the trial. These advantages should be communicated to ethics committees, who may have limited understanding of the design. 

In addition, researchers should carefully strike a balance between the information they give to patients (e.g., in patient information sheets) and the need to minimise potential biases that could be introduced by disclosing too much information. For instance, researchers should consider whether information disclosed may lead to participants who are recruited earlier being systematically different from those enrolled later. 

Tips on explaining the design to stakeholders

The main selling points of MAMS designs are the efficient use of research resources (e.g., infrastructure and patients) and ability to address multiple research questions in parallel, as several treatments can be contrasted under the same conditions in a single trial. As a result, futile treatments are filtered out and promising ones identified quickly to reduce the delay from clinical testing to clinical practice. This is true in comparison to running several traditional two-arm trials or a fixed multi-arm trial (i.e., without options for selection or stopping at an interim analysis).

Such efficiencies can be quantified under different scenarios with respect to the number of patients required, study durations and required research resources (see 1) . MAMS designs can be particularly useful in evaluating treatments in restricted populations (e.g., rare diseases) 2. Communicating this information to key stakeholders, such as sponsors, funders, ethics committees, regulators, and clinical colleagues, will help explain and, if necessary, justify the appropriate use of MAMS designs in practice.

References

1. Jaki et al. Multi-arm multi-stage trials can improve the efficiency of finding effective treatments for stroke : a case study and review of the literature. BMC Cardiovasc Disord. 2018;18:215.
2. Jazić et al. Design and analysis of drop-the-losers studies using binary endpoints in the rare disease setting. J Biopharm Stat. 2021;31(4):507–22.

Other considerations

We refer PANDA users to the discussion on general considerations that are also applicable across adaptive designs. Here, we have only highlighted a few considerations.

1. Appropriateness of the outcome for treatment selection

When the adaptation outcome is different from the primary outcome, it is essential for the adaptation outcome to be informative of the treatment effect on the primary outcome. Otherwise, the risk of dropping effective or selecting ineffective interventions will be inappropriately high. When choosing an adaptation outcome, the advice of clinical investigators and other stakeholders such as regulators and patients is important, and previous data (if available) should also be used to support the relationship between the adaptation and primary outcome. 

2. Choosing the number and timing of interim analyses

The usual considerations for designs with interim analyses apply, including how the study is to be powered and whether strong control of overall error rates is desired for the trial (see 1, 2, 3 for general discussion). The number of interim analyses should be feasible to implement against the potential benefits of conducting these analyses which are context-dependent (see general considerations).

In practice, there is little benefit in performing more than 4-5 interim analyses although there may be some exceptional circumstances. The number of interim analyses should be chosen to ensure sufficient information is available in order to make decisions about continuing the study and selecting treatments. At the same time, these analyses should be scheduled appropriately, as interim analyses that are undertaken too late reduce the efficiency of the design. Interim analyses should be spaced such that sufficient data is accrued between them for the additional analysis to be worth performing. One option to deal with this aspect is to use designs that optimise the timing and number of interim analyses using well-defined criteria 4, 5 (see general considerations). 

Finally, the first interim analysis should be scheduled to ensure there is sufficient outcome data to make reliable interim decisions.

References

1. Wason et al. Some recommendations for multi-arm multi-stage trials. Stat Methods Med Res. 2016;25(2):716–27.
2. Wason et al . Correcting for multiple-testing in multi-arm trials: is it necessary and is it done? Trials. 2014;15:364. 
3. Howard et al. Recommendations on multiple testing adjustment in multi-arm trials with a shared control group. Stat Methods Med Res. 2018;27(5):1513–30.
4. Bratton. Design issues and extensions of multi-arm multi-stage clinical trials. University College London. 2015.
5. Wason et al. Optimal design of multi-arm multi-stage trials. Stat Med. 2012;31(30):4269–79.

Some limitations and challenges

Despite several benefits of MAMS designs, there are specific issues to overcome (see 1, 2, 3 for a detailed discussion). Some challenges that apply across all trials with interim analyses also apply for MAMS (see general considerations). These include the pace of recruitment relative to the accrual of outcome data and its impact on the design. For instance, some planned interim analyses may be rendered obsolete when recruitment is too quick and follow-up period is relatively long (e.g., the second interim analysis of the PANACEA MAMS-TB trial). Furthermore, there is an increased risk of erroneously dropping potentially effective treatments at interim analyses if very few patients are included in the interim analysis. This risk could be lessened by using more stringent early stopping criterion. However, convincing the consumers of research findings may be challenging.

MAMS trials tend to require more resources upfront to aid set-up and conduct because of multiple treatment arms involved that are analysed at multiple stages, so ensuring all required resources are available at the right time is crucial. In addition, researchers should be prepared to recruit the maximum sample size (i.e., assuming no treatment arms will be dropped at interim analyses). 

In some cases, the commercial interest of sponsors or those owning intellectual property rights of competing interventions may undermine the feasibility of the MAMS trial as some stakeholders (e.g.,  drug companies) may not want head-to-head comparisons against competitors. Researchers should give themselves enough time at the planning stage to get relevant agreements in place. In addition, a clear preference for certain treatments over others (e.g., by participants and clinicians) can undermine the feasibility of the trial (e.g., patients unwilling to be allocated to certain treatments) and introduce biases (e.g., due to differential compliance and patient care).

There are some discussions and recommendations addressing statistical and practical considerations 3, 4, 8, including issues specific to seamless adaptive designs, which is a variant of the MAMS designs described above 5, 6, as well as some practical lessons learned 7. 

References

1. Millen et al. Adaptive trial designs: What are multiarm, multistage trials? Arch Dis Child Educ Pract Ed. 2019.
2. Jaki. Multi-arm clinical trials with treatment selection: what can be gained and at what price? Clin Investig. 2015;5(4):393–9.
3. Sydes et al. Issues in applying multi-arm multi-stage methodology to a clinical trial in prostate cancer: the MRC STAMPEDE trial. Trials. 2009;10:39.
4. Wason et al. Some recommendations for multi-arm multi-stage trials. Stat Methods Med Res. 2016;25(2):716–27.
5. Cuffe et al. When is a seamless study desirable? Case studies from different pharmaceutical sponsors. Pharm Stat. 2014;13(4):229–37.
6. Spencer et al. Operational challenges and solutions with Implementation of an adaptive seamless phase 2/3 study. J Diabetes Sci Technol. 2012;6(6):1296–304.
7. Chen et al. A seamless phase IIB / III adaptive outcome trial : design rationale and implementation challenges. 2015;12(1):84–90.
8. Maca at al. Adaptive seamless phase II/III designs - Background, operational aspects, and examples. Drug Inf J. 2006;40(4):463-473.

Examples of how MAMS trials are designed

Here, we use two real-life case studies that used frequentist methods for illustration. There are other several examples available in the literature 4, 7. Specifically, there are useful case studies that used Bayesian methods (e.g., 5, 6, 8). 'Rpact'  vignettes also cover step-by-step practical examples demonstrating the design and analysis of MAMS trials.  

1. TAILoR trial 1, 2

Below is an example of the TAILoR study which was aimed to assess the efficacy and safety of telmisartan in reducing insulin resistance in patients receiving combination antiretroviral therapy, and to identify the optimal dosage of telmisartan for further evaluation in a confirmatory trial.

General description

The primary outcome measure is the reduction in insulin resistance in the telmisartan-treated group(s) in comparison with the control group as measured by HOMA-IR. Patients will initially be randomised equally to receive either one of three doses of telmisartan (20, 40, and 80 mg) or no intervention (control). At the interim analysis, if one active dose group has a substantially higher mean reduction of 24 weeks HOMA-IR score than the control group, then the study will be stopped and that dose recommended for further testing in a future confirmatory trial. Otherwise, any active dose groups showing insufficient promise at the interim analysis will be dropped and the study continued with the remaining doses and control. If no dose shows sufficient promise at the interim analysis, the study will be stopped. If a particular dose(s) is found to be the single most promising at the interim analysis, but the interim results are not strong enough yet to trigger early stopping for efficacy, that dose(s) will be followed up along with the control for a further 24 weeks (total: 48 weeks); the study is continued after the interim analysis with one or more doses, and if at the final analysis the best performing dose is associated with a large enough reduction in 24 weeks HOMA-IR then that dose will be recommended for further testing. The sample size calculation method used does not require specification of the standard deviation of change in HOMA-IR scores which was unknown. To ensure equal proportions of gender and ethnic groups in each arm, randomisation will be stratified by gender and ethnicity (African and non-African).  

Design

The primary outcome is the difference between the baseline HOMA-IR score and the HOMA-IR score at 24 weeks. The design has been constructed under the assumption that for all patients this response is normally distributed with a common standard deviation.

The sample size calculation is based on a one-sided overall type I error of 5% and a power of 90%. Effect sizes are specified as the percentage chance of a patient on active treatment achieving a greater reduction in HOMA-IR score than a patient on control, as this specification does not require knowledge of the common standard deviation. The requirement is that, if a patient on the best active dose has a 65% chance of a better response than a patient on control, while patients on the other two active treatments have a 55% chance of showing a better response than a patient on control, then the best active dose should be recommended for further testing with 90% probability.

The decision rules for stopping an arm or the entire trial are based on the t-statistic comparing active arms to control in a pairwise fashion. A single interim analysis will be undertaken after half of the maximum number of patients’ outcomes has been observed. Any dose whose outcome is worse than control will be dropped from the study (critical value >0). If all active doses are dropped the study stops for lack of benefit. The critical values for recommending a treatment being taken to further testing at the interim and final analyses (-2.782 and -2.086, respectively) have been chosen to guarantee control of the type I error rate and power using a method described elsewhere (see 3). The maximum sample size of this study is 336 evaluable patients and may reduce depending on the outcome of the interim analysis. The study was designed to recruit a total of 374 patients to account for an anticipated 10% dropout rate (assumed equal across arms). 

Key message 

Note that parameterisation of the MAMS code below assumes a positive outcome means the new treatment is efficacious. In the TAILoR trial, it is the opposite - that is, a reduction in HOMA-IR score indicates a good treatment outcome. As such, the efficacy and futility stopping boundaries are switched around and correspond to the lower and upper boundaries, respectively.   

References

1. Pushpakom et al. Telmisartan and Insulin Resistance in HIV (TAILoR): Protocol for a dose-ranging phase II randomised open labelled trial of telmisartan as a strategy for the reduction of insulin resistance in HIV-positive individuals on combination antiretroviral therapy. BMJ Open. 2015;5(10).
2. Pushpakom et al. Telmisartan to reduce insulin resistance in HIV-positive individuals on combination antiretroviral therapy: the TAILoR dose-ranging Phase II RCT. Effic Mech Eval. 2019;6(6):1–168.
3. Magirr et al. A generalized Dunnett test for multi-arm multi-stage clinical studies with treatment selection. Biometrika. 2012;99(2):494–501.
4.  Brown et al. Multiple interventions for Diabetic Foot Ulcer Treatment Trial (MIDFUT): Study protocol for a randomised controlled trial. BMJ Open. 2020;10(4):e035947.
5. Suchting et al. Citalopram for treatment of cocaine use disorder: A Bayesian drop-the-loser randomized clinical trial. Drug Alcohol Depend. 2021;228:109054.
6. Rathnayaka et al. Drop-The-Loser: A practical bayesian adaptive design for a clinical trial of citalopram for cocaine use disorder. Clin Res Trials. 2017;3(4).
7. Krystal et al. Design of the national adaptive trial for PTSD-related insomnia (NAP study), VA cooperative study program (CSP) #2016. Contemp Clin Trials. 2021;109.
8. McCabe et al. The design and statistical aspects of VIETNARMS: A strategic post-licensing trial of multiple oral direct-acting antiviral hepatitis C treatment strategies in Vietnam. Trials. 2020;21.

R code:

## install package
install.packages("MAMS")

## load package
library("MAMS")

## to read help files
help(package="MAMS")
?mams
?mams.sim
The following code estimates sample size required per stage and arm, and stopping boundaries for a 4-arm, 2-stage design (3 experimental arms and control) with input parameters described above.
 
design <- mams(K=3, J=2, p=0.65, p0=0.55, ushape=function(a) return(c(4/3 * a, a)), 
               lshape="fixed", lfix=0, r=1:2, r0=1:2
        )
 
The following code simulates operating characteristics (type I error rate, expected sample size) under the null hypothesis. PANDA users may wish to increase the number of simulations and explore its impact on the precision of estimates.
 
mams.sim(nsim=10000, nMat=t(design$n * design$rMat), u=design$u, l=design$l, pv=rep(0.5, 3))
 
The following code simulate operating characteristics (power, expected sample size) under the “least favourable configuration” of the alternative hypothesis. 

mams.sim(nsim=10000, nMat=t(design$n * design$rMat), u=design$u, l=design$l, pv=c(0.65, rep(0.55, 2)))
 
 

2. STOP-OHSS trial (NIHR128137)


General description

Ovarian hyperstimulation syndrome (OHSS) often occurs in women who have over-responded to ovarian stimulation drugs. This is triggered by the effect of human chorionic gonadotropin (hCG) either administered during the course of treatment to trigger the maturation of the oocytes or produced naturally by a resulting pregnancy. The ovaries become enlarged and cystic, and fluid leaks into various body cavities. At present, treatment is only usually provided once the condition becomes severe. At this point, the patient is admitted to hospital as recommended in clinical guidelines. This inpatient management often includes drainage of ascites fluid (paracentesis), which can result in a significant improvement of the condition and an improvement in renal blood flow, urine output, and reversal of haematological abnormalities. About 3.1% to 8% of women undergoing fertility cycles (about 1800-4800 per year in the UK) experience moderate to severe OHSS.

OHSS is clinically classified into early and late. Early OHSS is usually caused by the ovarian stimulation drugs given during treatment, which tends to occur within 8 days after the final hCG dose is given. Late OHSS normally occurs 9 days or more after the administration of hCG and is caused by endogenous hCG of a resulting pregnancy (after embryo transfer). The overall aim of the study is to assess if earlier active outpatient management strategies resolve OHSS earlier and avoid the need for hospital admission when compared with usual conservative management. This will be assessed within two concurrent trials under the same infrastructure (umbrella trial). The first is a definitive trial within the early OHSS population, which is the focus here. The second is an exploratory efficacy trial using Bayesian analysis within the late OHSS population, which we will not discuss here.

Rationale

Evaluating new interventions in clinical trials in this limited population is challenging and calls for efficient trial designs. Researchers therefore used a three-arm two-stage (MAMS) design to evaluate the effects of two competing earlier active management interventions compared to a shared control simultaneously in a single trial with options to identify and stop intervention(s) early that are likely to fail to show benefit at the end of the trial. In this restricted trial population, due to the MAMS design researchers are able to address multiple research questions, make efficient use of research resources by focusing on interventions that are likely to benefit patients, possibly shorten the trial duration, and identify effective interventions quickly (if they exist) to benefit patients quicker compared to a series of separate two-arm fixed sample size trials. The design could minimise the number of women randomised to receive potentially ineffective intervention(s), which is desirable from an ethical perspective.

Design

The primary outcome is hospitalisation within 28 days of randomisation (yes/no). The proposed MAMS design is based on published adaptive methods 23,24. Researchers first explored a set of designs that minimise the expected sample size under the global null and alternative hypotheses using the ‘nstagebinopt’ Stata program 1. This gives the optimal number of stages and estimates the stagewise power and decision-making criteria to either drop futile arms, or declare an intervention arm effective at the final analysis for a specified set of desired statistical properties across all stages. We selected a feasible design with desired stagewise operating characteristics. Finally, we used the ‘nstagebin’ Stata program 1 to fully explore the operating characteristics and estimate the trial duration of the selected design presented here. In summary, the chosen design meets the following criteria:

  • feasibility of recruiting the maximum number of participants assuming no treatment arm will be dropped at any interim analysis;
  • sufficient interim data to inform treatment selection;
  • clinically meaningful treatment selection rule for dropping futile intervention(s). A preliminary health economics model suggested that an absolute reduction in hospitalisation attributed to the use of gonadotropin-releasing hormone (GnRH) antagonist and paracentesis would need to be greater than 5% and 7%, respectively, for them to be cost-effective. As a result, we chose a design with a selection rule to drop an arm if the absolute reduction in hospitalisation compared to usual care is below 6% range consistent with this preliminary health economics model;
  • a very high probability of selecting promising treatments at an interim analysis (if they exist);
  • a very small probability of a treatment being selected as promising at any interim analysis (when it is not);
  • a high probability of finding an effective treatment at the end of the trial (if it exists);
  • a very small probability of declaring ineffective treatments as effective at the end of the trial. 

Design assumptions

The average usual care hospitalisation rate was about 30% based on a preliminary survey of proposed trial sites. Earlier active management interventions have achieved low hospitalisation rates of around 0-8% based on uncontrolled small previous studies. Investigators, therefore, targeted a realistic 20% absolute reduction in hospitalisation (odds ratio, OR=0.259) for an intervention to be considered superior to usual care. This target 20% absolute reduction is realistic (previous studies have observed similar or greater effects) and, if observed, is big enough to change clinical practice. A recruitment rate of around eight women per month across the proposed 20 recruitment sites was viewed as realistic. Researchers aimed for a 2.5% one-sided familywise error rate at the end of the trial. A one-sided test was chosen because the direction of effect is essential for treatment selection. For exploring designs, 80%, 85% and 90% overall study power was used (the final design had 90% power). In addition, randomisation ratios of 1:1:1 and 2:1:1 (usual care to interventions), as well as two- and three-stage designs were explored (see Stata code below). Treatment selection at an interim analysis will be based on the primary outcome (hospitalisation within 28 days).

Sample size and operating characteristics for the selected design

The sample size was calculated assuming women with early OHSS will be randomised to usual care, outpatient paracentesis, or outpatient GnRH antagonist using 2:1:1 allocation ratio. The usual care is believed to be variable so randomisation was overloaded to this arm to get more data on the shared control. In addition, it reduces the maximum sample size for the MAMS design. 

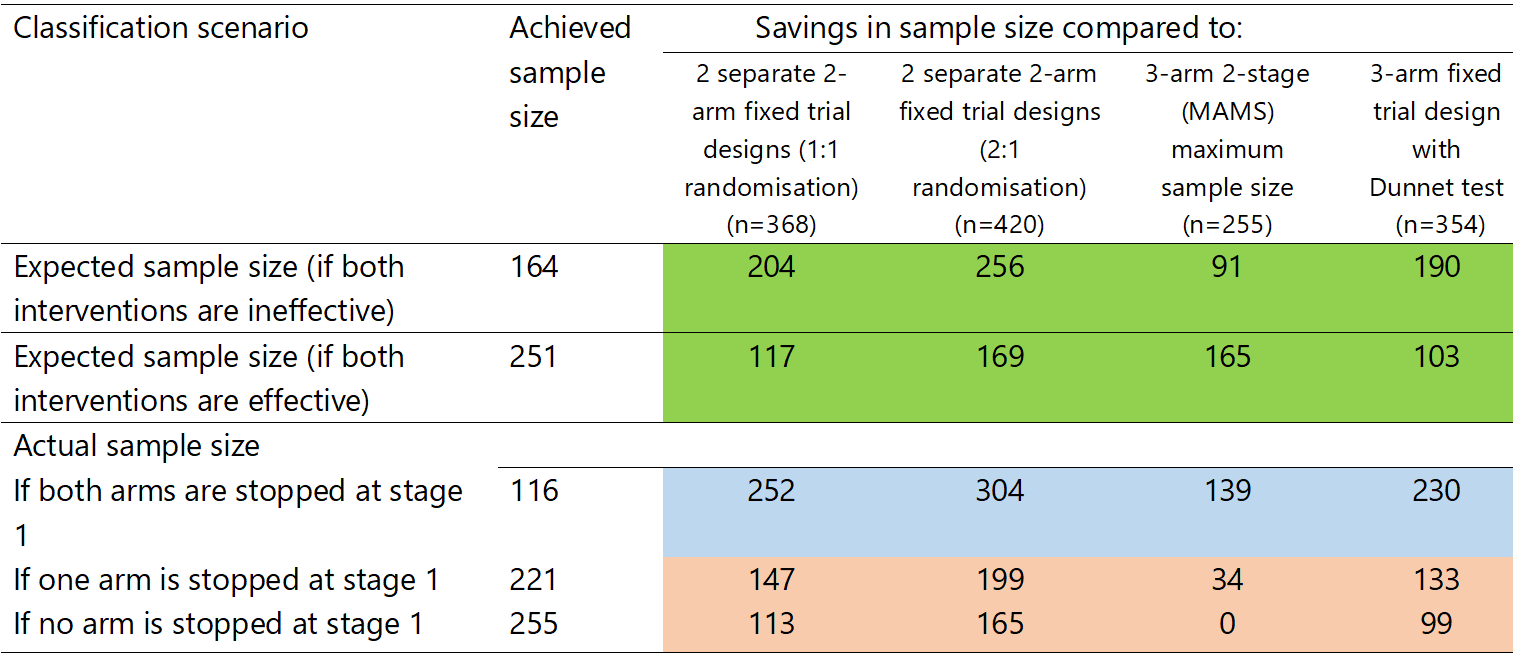
The maximum total sample size is 255 patients (~128: 64: 64 per arm). One interim analysis will be performed when 116 patients are recruited [58: 29: 29], which is about 46% of the maximum sample size. At this stage, at least 108 (42%) would have accrued the primary outcome data for interim analysis (54: 27: 27). If both interventions are selected, the final analysis will be performed after the accrual of data from 255 patients. If one intervention is selected, the final analysis will be performed after the accrual of data from 192 participants (128: 64 in remaining arms). There is a possibility to stop the entire trial early if both paracentesis and GnRH antagonist are dropped at the interim analysis. The trial does not allow for early stopping for efficacy at the interim analysis. If only one arm is selected at stage 1, randomisation will be consequently updated to 2:1 (usual care to remaining arm).

The trial will have a stagewise power for pairwise comparisons at the interim and final analysis of 96% and 92%, respectively. Very high power at stage 1 was chosen to give a high chance of carrying forward promising intervention(s) if they exist. The familywise error rate is controlled at 2.45% (one-sided) within a standard error of 0.3% (estimated via simulation methods). This assumes that all the arms reach the final analysis.

An intervention will be deemed futile at the interim analysis if the p-value corresponding to the pairwise one-sided test of that intervention versus usual care is ≥0.27, which is approximately equivalent to an absolute reduction in hospitalisation of about ≤6% (30% to 24%; OR=0.737). This effect is less than a third of the targeted 20% absolute reduction, which is reasonable for an efficacy signal and in the region likely to be cost effective. At the final analysis, an intervention that passes the interim hurdle will be deemed superior to usual care if a pairwise one-sided test p-value is <0.014.

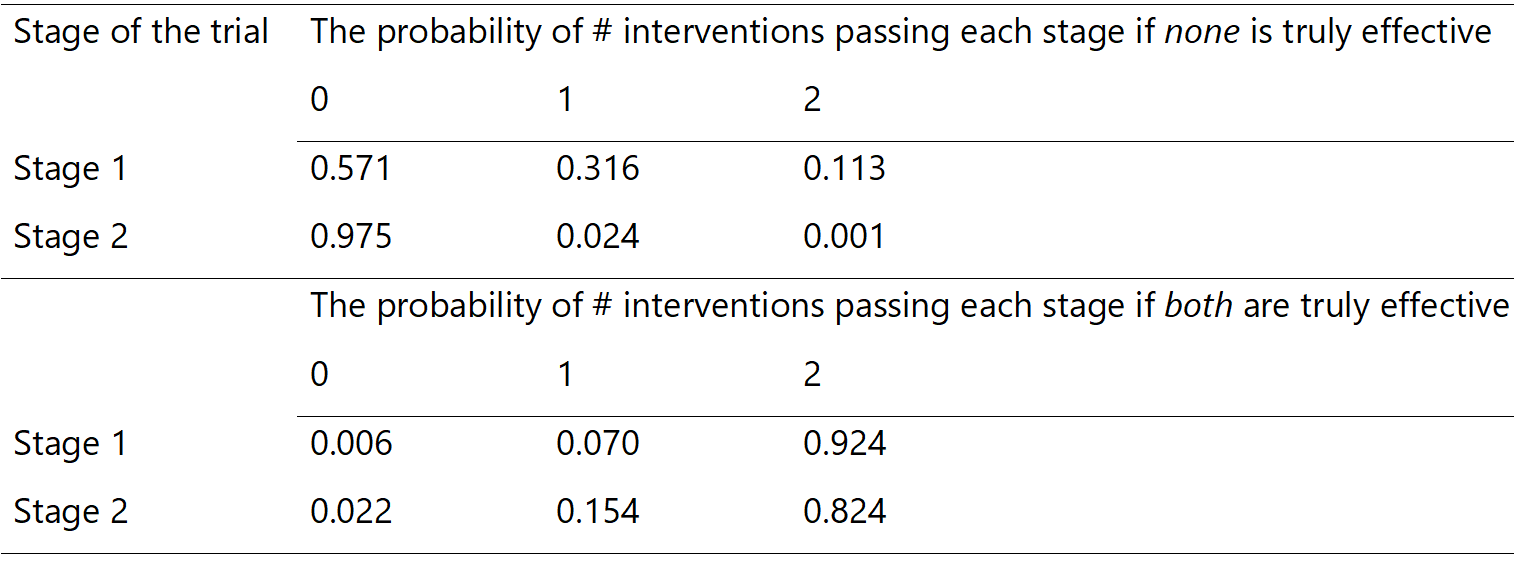
It is useful to know the chances of making incorrect decisions at each stage (interim and final analysis, see Table 1). Here, the probabilities of selecting promising treatment(s) at stage 1 and claiming evidence of effectiveness at the final analysis (stage 2) under two scenarios are presented: neither study intervention is truly effective (global null), or both study interventions are truly effective (global alternative). For example, if none of the interventions are truly effective, there is a:

  • 57.1% chance of stopping the entire trial at stage 1 (i.e. no intervention will be selected to proceed to stage 2),
  • 31.6% chance that only one intervention will be incorrectly deemed promising to proceed to 2,
  • Only 11.3% chance for incorrectly selecting both interventions as promising to proceed to stage 2.
On the other hand, if both interventions are truly effective, there is a very: 

  • high (92.4%) chance of selecting both interventions as promising at stage 1 to proceed to stage 2,
  • small (0.6%) chance of dropping both interventions at stage 1 (stopping the entire trial),
  • high (97.8%) chance of declaring at least one of the interventions as effective at the end of the trial.
In summary, this design offers 57.1% chance of dropping futile interventions, whilst allowing truly effective interventions to pass the hurdle at the interim analysis with very high probability. In reality, one would also want to explore another scenario which is not presented here for brevity, where one intervention is truly effective and the other one is truly ineffective.

Table 1.

Table 1. Performance of the design in treatment selection and finding effective interventions.

Performance of the design in treatment selection and finding effective interventions.

Some quantifiable benefits

 Table 2 shows that the MAMS is always superior to an alternative series of two-arm fixed sample size designs. In addition, there are considerable savings in patients under a few scenarios (see Table 2). If we account for the probabilities of stopping (in Table 1), the expected total sample size assuming no interventions are effective or both interventions are effective is 164 or 251 participants, respectively. Thus, if there are no effective interventions, this design will reduce the expected sample size by about 91 women and provide significant cost savings by concluding the trial approximately 11.4 months early. Table 2 summarises the savings in the total number of patients assuming an average sample size and stopping scenarios.

Table 2.

Table 2. Sample size savings

Sample size savings.

Stata code:

// install packages 
ssc install nstagebin 
ssc install nstagebinopt 

// to read help files
chelp nstagebinopt 
chelp nstagebin 

// exploring 3-arm and 2-stage designs: 
Click this hyperlink to access the full code on github


// final selected design
nstagebin, nstage(2) accrate(8 8) alpha(0.27 0.014)             /// 
             power(0.96 0.92) arms(3 3) theta0(0)               /// 
             theta1(-0.20) ctrlp(0.3) fu(0.92) ltfu(0) tunit(4) /// 
             aratio(0.5) probs ess extrat(0) seed(25)
A SAS code exploring the properties of this design and a detailed simulation report are accessible via github.

Interim analysis/monitoring 

The primary endpoint, hospitalisation within 28 days (yes/no), will be modelled using a multiple logistic regression adjusted for stratification factors (site and severity of early OHSS – moderate and severe). The intervention effect (OR) with the uncertainty of outpatient paracentesis and GnRH antagonist compared to usual care will be obtained via pairwise hypothesis tests. The absolute risk differences in hospitalisation will be post-estimated after logistic regression using the delta method via margins 1. A treatment arm will proceed to stage 2 if a one-sided p-value from a logistic regression model is less or equal 0.27 (corresponding to an absolute risk reduction of around 6% in favour of the new intervention). 

Final analysis 

A similar model as for the interim analysis will be used in the final analysis, and an intervention will be declared statistically significant if a one-sided p-value is less than 0.014. A simulation study was performed to investigate the performance of naïve (maximum likelihood, ML) and bias-adjusted estimators in relation to the extent of bias and confidence interval coverage if the trial progresses beyond interim analysis. Bias-adjusted estimators investigated used Rao-Blackwellisation approach 2. It should be noted that these bias-adjusted estimators do not eliminate bias or provides exact confidence interval coverage but aim to reduce the bias and improve confidence interval coverage. Simulations were conducted under several scenarios of the observed hospitalisation event rates in each treatment arm. PANDA users are encouraged to read a detailed simulation report with conclusions. For statistical implementation, related SAS code used is accessible via github.

In summary, bias adjustment using Rao-Blackwellisation was shown to reduce bias and lead to reasonably accurate confidence intervals and it was deemed worth applying to reduce bias compared to using naïve (ML) estimators if the trial progresses beyond interim analysis. If there is no promising treatment and the trial is stopped early at the interim analysis, the ML estimators using interim data will be sufficient. 

Some limitations

Due to the limitation of the feasible maximum number of patients that can be recruited, there is a region of the treatment effect where the interventions (if truly effective) can result in marked healthcare economic savings but the study will have insufficient power to demonstrate such small to moderate treatment effects. It is debatable whether such small to moderate effects will be able to change practice. 

References

1. Norton et al. Computing adjusted risk ratios and risk differences in Stata. Stata J. 2013;13(3).
2. Whitehead et al. Estimation of treatment effects following a sequential trial of multiple treatments. Stat Med. 2020;39(11):1593–609.